
【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.

(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
科目:初中数学 来源: 题型:
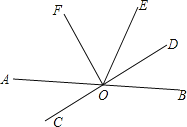
【题目】如图,直线AB与CD相交于点O,OD平分∠BOE,∠FOD=90°,问OF是∠AOE的平分线吗?请你补充完整小红的解答过程.
探究:
(1)当∠BOE=70°时,
∠BOD=∠DOE=![]() ,
,
∠EOF=90°﹣∠DOE= °,
而∠AOF+∠FOD+∠BOD=180°,
所以∠AOF+∠BOD=180°﹣∠FOD=90°,
所以∠AOF=90°﹣∠BOD= °,
所以∠EOF=∠AOF,OF是∠AOE的平分线.
(2)参考上面(1)的解答过程,请你证明,当∠BOE为任意角度时,OF是∠AOE的平分线.
(3)直接写出与∠AOF互余的所有角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的边OB上的一点.
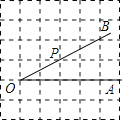
(1)过点P画OB的垂线,交OA于点C,
(2)过点P画OA的垂线,垂足为H,
(3)线段PH的长度是点P到 的距离,线段 是点C到直线OB的距离.
(4)因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 (用“<”号连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰三角形的一个内角为70°,则另两个内角的度数是( )
A. 55°,55° B. 70°,40°
C. 55°,55°或70°,40° D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游景点的门票价格如下表:
购票人数/人 | 1﹣50 | 51﹣100 | 100以上 |
每人门票价/元 | 80 | 75 | 70 |
某校八年级(1)、(2)两班共100多人计划去游览该景点,其中(1)班人数少于50人,(2)班人数有50多人,如果两班都以班为单位单独购票,则一共支付7965元;如果两班联合起来作为一个团体购票,则只需花费7210元.两个班各有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.无限小数是无理数;
B.零是整数,但不是正数,也不是负数;
C.分数包括正分数、负分数和零;
D.有理数不是正数就是负数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).

(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN= 时,结论AM=MN仍然成立.(直接写出答案,不需要证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com