
【题目】已知:如图,△ABC中,∠A=45°,AB=6,AC=![]() ,点D、E、F分别是三边AB、BC、CA上的点,则△DEF周长的最小值是______.
,点D、E、F分别是三边AB、BC、CA上的点,则△DEF周长的最小值是______.

【答案】![]()
【解析】
如图,作E关于AB的对称点,作E关于AC的对称点N,连接AE,MN,MN交AB于D,交AC于F,作AH⊥BC于H,CK⊥AB于K.由对称性可知:DE=DM,FE=FN,AE=AM=AN,推出△DEF的周长DE+EF+FD=DM+DF+FN,推出当点E固定时,此时△DEF的周长最小,再证明△MNA是等腰直角三角形,推出MN=![]() AE,推出当AE的值最小时,MN的值最小,求出AE的最小值即可解决问题;
AE,推出当AE的值最小时,MN的值最小,求出AE的最小值即可解决问题;
解:如图,作E关于AB的对称点,作E关于AC的对称点N,连接AE,MN,MN交AB于D,交AC于F,作AH⊥BC于H,CK⊥AB于K.
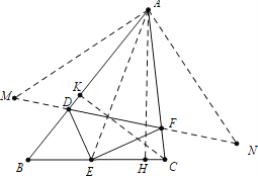
由对称性可知:DE=DM,FE=FN,AE=AM=AN,
∴△DEF的周长DE+EF+FD=DM+DF+FN,
∴当点E固定时,此时△DEF的周长最小,
∵∠BAC=45°,∠BAE=∠BAM,∠CAE=∠CAN,
∴∠MAN=90°,
∴△MNA是等腰直角三角形,
∴MN=![]() AE,
AE,
∴当AE的值最小时,MN的值最小,
∵AC=4![]() ,
,
∴AK=KC=4,
∵AB=6,
∴BK=AB-AK=2,
在Rt△BKC中,∵∠BKC=90°,BK=2,CK=4,
∴BC=![]() =2
=2![]() ,
,
∵![]() BCAH=
BCAH=![]() ABCK,
ABCK,
∴AH=![]() ,
,
根据垂线段最短可知:当AE与AH重合时,AE的值最小,最小值为![]() ,
,
∴MN的最小值为![]() ,
,
∴△DEF的周长的最小值为![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】一商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价a元,则平均每天销售数量为 件.(用含a的代数式表示)
(2)当每件商品降价多少元时,该商店每天销售利润为1200元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种)
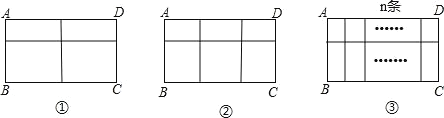
设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
(1)在图①中,如果不锈钢材料总长度为 12 米,当x为多少时,矩形框架ABCD的面积为 3 平方米?
(2)在图②中,如果不锈钢材料总长度为 12 米,当x为多少时,矩形架ABCD的面积S最大?最大面积是多少?
(3)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,那么当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.
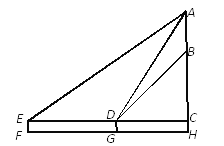
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有100棵橙子树,平均每棵结600个橙子.现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就要减少.根据经验估计,每增种1棵树,平均每棵树就少结5个橙子.设果园增种x棵橙子树,果园橙子的总产量为y个.
(1)求y与x之间的关系式;
(2)增种多少棵橙子树,可以使橙子的总产量在60 420个以上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在北部湾经济区农业示范基地采购A,B两种农产品,已知A种农产品每千克的进价比B种多2元,且用24000元购买A种农产品的数量(按重量计)与用18000元购买B种农产品的数量(按重量计)相同.
(1)求A,B两种农产品每千克的进价分别是多少元?
(2)该公司计划购进A,B两种农产品共40吨,并运往异地销售,运费为500元/吨,已知A种农产品售价为15元/kg,B种农产品售价为12元/kg,其中A种农产品至少购进15吨且不超过B种农产品的数量,问该公司应如何采购才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
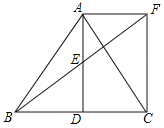
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com