
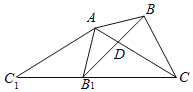
【题目】如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△A1B1C1,当C,B1,C1三点共线时,旋转角为α,连接BB1,交于AC于点D,下面结论:
①△AC1C为等腰三角形;②CA=CB1;③α=135°;④△AB1D∽△ACB1;⑤![]() =
=![]() 中,正确的结论的序号为______.
中,正确的结论的序号为______.
【答案】①②④⑤
【解析】
首先根据旋转的性质得出AC1=AC,从而结论①可判断;再通过三角形内角和定理及旋转角的计算对②③作出判断;通过∠AB1D=∠ACB1=30°,∠B1AD=∠CA B1,,判定△AB1D∽△ACB1;通过证明△ABD∽△B1CD,利用相似三角形的性质列式计算对⑤作出判断.
由旋转的性质可知:AC1=AC,
∴△AC1C为等腰三角形,即①正确;
∵∠ACB=30°,
∴∠C1=∠ACB1=30°,
又∵B1AC1=∠BAC=45°,
∴∠AB1C=75°,
∴∠CAB1=180°﹣75°﹣30°=75°,
∴CA=CB1;即②正确;
∵∠CAC1=∠CAB1+∠B1AC1=120°,
∴旋转角α=120°,故③错误;
∵∠BAC=45°,
∴∠BAB1=45°+75°=120°,
∵AB=AB1,
∴∠AB1B=∠ABD=30°,
在△AB1D与△ACB1中,
∵∠AB1D=∠ACB1=30°,∠B1AD=∠CA B1,
∴△AB1D∽△ACB1,即④正确;
在△ABD与△B1CD中,
∵∠ABD=∠ACB1,∠ADB=∠CDB1,
∴△ABD∽△B1CD,
∴![]() =
=![]() ,
,
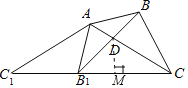
∴∠DB1C=∠DAB=45°,
过点D作DM⊥B1C,
设DM=x,则B1M=x,B1D=![]() x,DC=2x, CM=
x,DC=2x, CM=![]() x,
x,
∴AC=B1C=(![]() +1)x,
+1)x,
∴AD=AC﹣CD=(![]() ﹣1)x,
﹣1)x,
∴![]() =
=![]() =
=![]() =
=![]() ,即⑤正确.
,即⑤正确.
故答案为:①②④⑤.


科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 分别为x轴,y轴相交于A,B两点,点P(0,m)是y轴上一个动点,若以点P为圆心的圆P与x轴和直线l都相切,则m的值是_______.
分别为x轴,y轴相交于A,B两点,点P(0,m)是y轴上一个动点,若以点P为圆心的圆P与x轴和直线l都相切,则m的值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=![]() ,的图象和性质进行了探究探究过程如下,请补充完成:
,的图象和性质进行了探究探究过程如下,请补充完成:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.请直接写出m,n的值:m= ;n= .
x | … | ﹣2 | ﹣1 | 0 |
|
|
| n | 2 | 3 | 4 | … |
y | … |
| m | 0 | ﹣1 | ﹣3 | 5 | 3 | 2 |
|
| … |
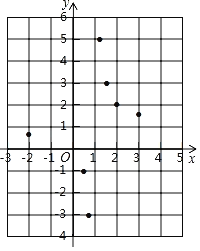
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)通过观察函数的图象,小明发现该函数图象与反比例函数y=![]() (k>0)的图象形状相同,是中心对称图形,且点(﹣1,m)和(3,
(k>0)的图象形状相同,是中心对称图形,且点(﹣1,m)和(3,![]() )是一组对称点,则其对称中心的坐标为 .
)是一组对称点,则其对称中心的坐标为 .
(5)当2≤x≤4时,关于x的方程kx+![]() =
=![]() 有实数解,求k的取值范围.
有实数解,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:对于函数y,若当![]() ,函数值y满足
,函数值y满足![]() ,且满足
,且满足![]() ,则称此函数为“k属和合函数”
,则称此函数为“k属和合函数”
例如:正比例函数![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() ,求得:
,求得:![]() ,所以函数
,所以函数![]() 为“3属和合函数”.
为“3属和合函数”.
(1)①一次函数![]() 为“k属和合函数”,则k的值为______,
为“k属和合函数”,则k的值为______,
②若一次函数![]() 为“1属和合函数”,求a的值;
为“1属和合函数”,求a的值;
(2)反比例函数![]() (
(![]() ,
,![]() 且
且![]() )是“k属和合函数”,且
)是“k属和合函数”,且![]() ,请求出
,请求出![]() 的值;
的值;
(3)已知二次函数![]() ,当
,当![]() 时,y是“k属和合函数”,求k的取值范围.
时,y是“k属和合函数”,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情防控期间.某小区卫生所决定购买A,B两种口罩.以满足小区居民的需要.若购买A种口罩9包,B种口罩4包,则需要700元;若购买A种口罩3包.B种口罩5包.则需要380元.
(1)购买人A,B两种口罩每包各需名少元?
(2)卫生所准备购进这两种口罩共90包,并且A种口罩包数不少于B种口罩包数的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/千克,根据销售情况发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间满足如下表所示的一次函数关系:
(元/千克)之间满足如下表所示的一次函数关系:
(1)写出销售量![]() 与售价
与售价![]() 之间的函数关系式;
之间的函数关系式;
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式,并求出当售价为多少元时,当天的获利最大,最大利润是多少?
之间的函数关系式,并求出当售价为多少元时,当天的获利最大,最大利润是多少?
售价 | … | 25 | 24.5 | 22 | … |
销售量 | … | 35 | 35.5 | 38 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com