
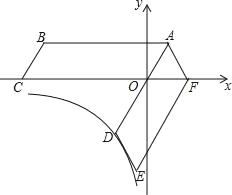
【题目】如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将平行四边形 ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴的正半轴上.若点D在反比例函数y=![]() (x<0)的图象上,则k的值为( )
(x<0)的图象上,则k的值为( )
A.4![]() B.12C.8
B.12C.8![]() D.6
D.6
【答案】A
【解析】
结合图形可知,作DM⊥x轴,MO为横坐标,MD为纵坐标,则求点D坐标转化为求MO和MD的长度;已知四边形ADEF是由四边形ABCO旋转而来,则∠BAO=∠OAF,AO=AF,根据平行四边形性质可知AB∥OC,则可得∠BAO=∠AOF,进而可得∠AOF=60°=∠DOM;根据OA=2,AB=6可得OD=4,再通过三角函数即可求出MO和MD,据此可得答案.
解:如图,作DM⊥x轴,

由题意∠BAO=∠OAF,AO=AF,AB∥OC,
∴∠BAO=∠AOF=∠OAF=∠AFO,
∴∠AOF=60°=∠DOM.
∵OD=AD-OA=AB-OA=6-2=4,
∴∠ODM=30,
∴MO=2,MD=![]() =2
=2![]() ,
,
∴D(-2,-2![]() ),
),
∴k=-2×(-2![]() )=4
)=4![]() .
.
故选A.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+4ax+c的最大值为4,且图象过点(﹣3,0).
(1)求二次函数解析式;
(2)若将该二次函数的图象绕着原点旋转180°,请直接写出旋转后图象的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
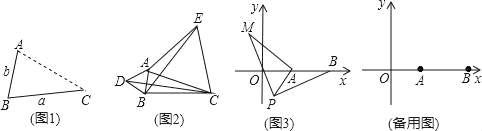
【题目】(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.填空:
当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=4,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(6,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c,函数值y与自变量x之间的部分对应值如下表:
x | … | ﹣4 | ﹣1 | 0 | 1 | … |
y | … | ﹣2 | ﹣1 | ﹣2 | ﹣7 | … |
(1)此二次函数图象的对称轴是直线,此函数图象与x轴交点个数为 .
(2)求二次函数的函数表达式;
(3)当﹣5<x<﹣1时,请直接写出函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制.中小学楼梯宽度的范围是260mm~300mm含(300mm),高度的范围是120mm~150mm(含150mm).如图是某中学的楼梯扶手的截面示意图,测量结果如下:AB,CD分别垂直平分踏步EF,GH,各踏步互相平行,AB=CD,AC=900mm,∠ACD=65°,试问该中学楼梯踏步的宽度和高度是否符合规定.(结果精确到1mm,参考数据:sin65°≈0.906,cos65°≈0.423)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在公园有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为![]() 公分.敏敏观察到高度
公分.敏敏观察到高度![]() 公分矮圆柱的影子落在地面上,其影长为
公分矮圆柱的影子落在地面上,其影长为![]() 公分;而高圆柱的部分影子落在墙上,如图所示.
公分;而高圆柱的部分影子落在墙上,如图所示.

已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
(1)若敏敏的身高为![]() 公分,且此刻她的影子完全落在地面上,则影长为多少公分?
公分,且此刻她的影子完全落在地面上,则影长为多少公分?
(2)若同一时间量得高圆柱落在墙上的影长为![]() 公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com