已知直线y=kx+3经过点A（-4，0），且与y轴交于点B，点O为坐标原点．
（1）求k的值；
（2）求点O直线AB的距离；
（3）过点C（0，1）的直线把△AOB的面积分成相等的两部分，求这条直线的函数关系式．

解：（1）依题意得：-4k+3=0，
解得k= $\text{[math]}$ ；

（2）由（1）得y= $\text{[math]}$ x+3，
当x=0时，y=3，即点B的坐标为（0，3）．
如图，过点O作OP⊥AB于P，则线段OP的长即为点O直线AB的距离．
∵S_△AOB= $\text{[math]}$ AB•OP= $\text{[math]}$ OA•OB，
∴OP= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ；

（3）设所求过点C（0，1）的直线解析式为y=mx+1．
S_△AOB= $\text{[math]}$ OA•OB= $\text{[math]}$ ×4×3=6．
分两种情况讨论：
①当直线y=mx+1与OA相交时，设交点为D，则
S_△COD= $\text{[math]}$ OC•OD= $\text{[math]}$ ×1×OD=3，
解得OD=6．
∵OD＞OA，
∴OD=6不合题意舍去；
②当直线y=mx+1与AB相交时，设交点为E，则

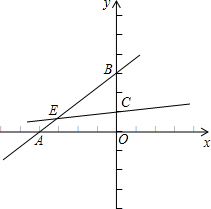
S_△BCE= $\text{[math]}$ BC•|x_E|= $\text{[math]}$ ×2×|x_E|=3，
解得|x_E|=3，
则x_E=-3，
当x=-3时，y= $\text{[math]}$ x+3= $\text{[math]}$ ，
即E点坐标为（-3， $\text{[math]}$ ）．
将E（-3， $\text{[math]}$ ）代入y=mx+1，得-3m+1= $\text{[math]}$ ，
解得m= $\text{[math]}$ ．
故这条直线的函数关系式为y= $\text{[math]}$ x+1．
分析：（1）因为直线y=kx+3经过点A（-4，0），所以把点A的坐标直接代入即可求出k的值；
（2）过点O作OP⊥AB于P，则线段OP的长即为点O直线AB的距离，根据△AOB的面积不变列式，即可求解；
（3）设所求过点C（0，1）的直线解析式为y=mx+1，△AOB被分成的两部分面积相等，那么被分成的两部分都应该是△AOB的面积的一半，分两种情况讨论：①直线y=mx+1与OA相交；②直线y=mx+1与AB相交．
点评：本题考查了运用待定系数法求函数的解析式，三角形的面积，一次函数的性质，难度适中，进行分类讨论是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

12、已知直线y=kx+b经过第一、二、四象限，则直线y=bx+k经过（　　）

A、第一、三、四象限

B、第一、二、三象限

C、第一、二、三象限

D、第二、三、四象限

查看答案和解析>>

科目：初中数学 来源： 题型：

（2012•义乌市）如图1，已知直线y=kx与抛物线y=-

x2+

交于点A（3，6）．
（1）求直线y=kx的解析式和线段OA的长度；
（2）点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N．试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；
（3）如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？