
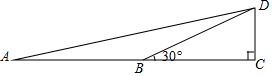
 如图,∠C=90°,∠DBC=30°,AB=BD,根据此图求tan15°的值.
如图,∠C=90°,∠DBC=30°,AB=BD,根据此图求tan15°的值.  备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
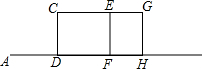 如图,A、B在一直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后达点H,此时他(GH)处于灯光正下方.
如图,A、B在一直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后达点H,此时他(GH)处于灯光正下方.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
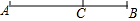 如图,点C在线段AB上,$\frac{AC}{AB}$=$\frac{CB}{AC}$,AB=1,AC=x,则x满足方程(整理成一般形式):x2+x-1=0,解之可求得线段AC=$\frac{-1+\sqrt{5}}{2}$,∴$\frac{AC}{AB}$=$\frac{-1+\sqrt{5}}{2}$=0.618.(精确到0.001)
如图,点C在线段AB上,$\frac{AC}{AB}$=$\frac{CB}{AC}$,AB=1,AC=x,则x满足方程(整理成一般形式):x2+x-1=0,解之可求得线段AC=$\frac{-1+\sqrt{5}}{2}$,∴$\frac{AC}{AB}$=$\frac{-1+\sqrt{5}}{2}$=0.618.(精确到0.001)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(+5)和-5 | B. | -(-5)和5 | C. | (-$\frac{1}{2}$) 与-2 | D. | +|+8|和-(+8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com