
ЗжЮі ЃЈ1ЃЉЯШАбРЈКХФкЭЈЗжКЭГ§ЗЈдЫЫуЛЏЮЊГЫЗЈдЫЫуЕУЕНдЪН=[$\frac{aЃЈa-2ЃЉ}{ЃЈa+2ЃЉЃЈa-2ЃЉ}$+$\frac{1}{ЃЈa+2ЃЉЃЈa-2ЃЉ}$]•$\frac{a+2}{a-1}$+$\frac{1}{a-2}$ЃЌдйМЦЫуРЈКХФкЕФМгЗЈдЫЫуКѓдМЗжЃЌНгзХНјааЭЌЗжФИЕФМгЗЈдЫЫуЃЌШЛКѓАбaЕФжЕДњШыМЦЫуМДПЩЃЛ
ЃЈ2ЃЉЯШАбЗжФИвђЪНЗжНтКѓдМЗжЃЌдйНјааЭЈЗжКЭЭЌЗжФИЕФМгЗЈдЫЫуЕУЕНдЪН=$\frac{1}{a-3}$ЃЌНгзХИљОнШ§НЧаЮШ§БпЕФЙиЯЕЕУЕН1ЃМaЃМ5ЃЌШЛКѓИљОнЗжЪНгавтвхЕФЬѕМўЕУЕНaЕФжЕЮЊ4ЃЌзюКѓАбa=4ДњШыМЦЫуМДПЩЃЛ
ЃЈ3ЃЉЯШАбРЈКХФкЭЈЗжКЭГ§ЗЈдЫЫуЛЏЮЊГЫЗЈдЫЫуЕУЕНдЪН=[$\frac{{x}^{2}}{xЃЈx-2ЃЉ}$-$\frac{4}{xЃЈx-2ЃЉ}$]•$\frac{xЃЈx-1ЃЉ}{x+2}$ЃЌдйМЦЫуРЈКХФкЕФМђЗЈдЫЫуКѓдМЗжЕУЕНдЪН=x-1ЃЌШЛКѓНтЗНГЬx2-x-2=0КЭИљОнЗжЪНгавтвхЕФЬѕМўЕУЕНx=-1ЃЌдйАбx=-1ДњШыМЦЫуМДПЩЃЎ
НтД№ НтЃКЃЈ1ЃЉдЪН=[$\frac{aЃЈa-2ЃЉ}{ЃЈa+2ЃЉЃЈa-2ЃЉ}$+$\frac{1}{ЃЈa+2ЃЉЃЈa-2ЃЉ}$]•$\frac{a+2}{a-1}$+$\frac{1}{a-2}$
=$\frac{ЃЈa-1ЃЉ^{2}}{ЃЈa+2ЃЉЃЈa-2ЃЉ}$•$\frac{a+2}{a-1}$+$\frac{1}{a-2}$
=$\frac{a-1}{a-2}$+$\frac{1}{a-2}$
=$\frac{a}{a-2}$ЃЌ
ЕБa=2+$\sqrt{2}$ЪБЃЌдЪН=$\frac{2+\sqrt{2}}{2+\sqrt{2}-2}$=$\sqrt{2}$+1ЃЛ
ЃЈ2ЃЉдЪН=$\frac{a}{ЃЈa+2ЃЉЃЈa-2ЃЉ}$•$\frac{a+2}{aЃЈa-3ЃЉ}$+$\frac{1}{a-2}$
=$\frac{1}{ЃЈa-2ЃЉЃЈa-3ЃЉ}$+$\frac{a-3}{ЃЈa-2ЃЉЃЈa-3ЃЉ}$
=$\frac{a-2}{ЃЈa-2ЃЉЃЈa-3ЃЉ}$
=$\frac{1}{a-3}$ЃЌ
Ёпaгы2ЃЌ3ЙЙГЩЁїABCЕФШ§БпЃЌ
Ёр1ЃМaЃМ5ЃЌ
ЖјaЮЊећЪ§ЃЌ
Ёрa=2ЃЌ3ЃЌ4ЃЌ
Ёпa-2Ёй0Чвa-3Ёй0ЃЌ
ЁрaЕФжЕЮЊ4ЃЌ
ЕБa=4ЪБЃЌдЪН=$\frac{1}{4-3}$=1ЃЛ
ЃЈ3ЃЉдЪН=[$\frac{{x}^{2}}{xЃЈx-2ЃЉ}$-$\frac{4}{xЃЈx-2ЃЉ}$]•$\frac{xЃЈx-1ЃЉ}{x+2}$
=$\frac{ЃЈx+2ЃЉЃЈx-2ЃЉ}{xЃЈx-2ЃЉ}$•$\frac{xЃЈx-1ЃЉ}{x+2}$
=x-1ЃЌ
НтЗНГЬx2-x-2=0ЕУx1=2ЃЌx2=-1ЃЌ
Жјx-2Ёй0ЃЌ
Ёрx=-1ЃЌДЫЪБдЪН=-1-1=-2ЃЎ
ЕуЦР БОЬтПМВщСЫЗжЪНЕФЛЏМђЧѓжЕЃКЯШАбЗжЪНЛЏМђКѓЃЌдйАбЗжЪНжаЮДжЊЪ§ЖдгІЕФжЕДњШыЧѓГіЗжЪНЕФжЕЃЎдкЛЏМђЕФЙ§ГЬжавЊзЂвтдЫЫуЫГађКЭЗжЪНЕФЛЏМђЃЎЛЏМђЕФзюКѓНсЙћЗжзгЁЂЗжФИвЊНјаадМЗжЃЌзЂвтдЫЫуЕФНсЙћвЊЛЏГЩзюМђЗжЪНЛђећЪНЃЎзЂвтЗжЪНгавтвхЕФЬѕМўЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
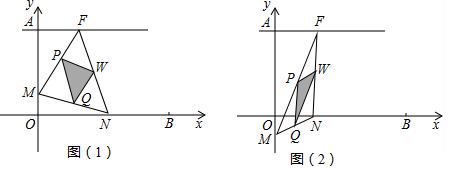
| AЃЎ | 1Иі | BЃЎ | 2Иі | CЃЎ | 3Иі | DЃЎ | 4Иі |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | Ъ§зж0вВЪЧЕЅЯюЪН | BЃЎ | ЕЅЯюЪНaЕФЯЕЪ§гыДЮЪ§ЖМЪЧ1 | ||
| CЃЎ | xyЪЧЖўДЮЕЅЯюЪН | DЃЎ | -$\frac{ab}{3}$ЕФЯЕЪ§ЪЧ-3 |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com