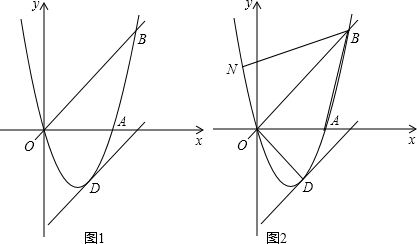
解:(1)∵A(3,0)、B(4,4)、O(0,0)在抛物线y=ax
2+bx+c (a≠0)上.
∴

,
解得:

,
故抛物线的解析式为:y=x
2-3x;
(2)设直线OB的解析式为y=k
1x( k
1≠0),
由点B(4,4)得
4=4 k
1,
解得k
1=1.
∴直线OB的解析式为y=x,∠AOB=45°.
∵B(4,4),
∴点B向下平移m个单位长度的点B′的坐标为(4,0),
故m=4.
∴平移m个单位长度的直线为y=x-4.
解方程组

解得:

,
∴点D的坐标为(2,-2).
(3)∵直线OB的解析式y=x,且A(3,0).
∵点A关于直线OB的对称点A′的坐标为(0,3).
设直线A′B的解析式为y=k
2x+3,此直线过点B(4,4).
∴4k
2+3=4,
解得 k
2=

.
∴直线A′B的解析式为y=

x+3.
∵∠NBO=∠ABO,∴点N在直线A′B上,
设点N(n,

n+3),又点N在抛物线y=x
2-3x上,
∴

n+3=n
2-3n.
解得 n
1=

,n
2=4(不合题意,舍去),
∴点N的坐标为(-

,
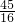
).

如图,将△NOB沿x轴翻折,得到△N
1OB
1,
则 N
1 (-

,-
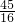
),B
1(4,-4).
∴O、D、B
1都在直线y=-x上.
∵△P
1OD∽△NOB,
∴△P
1OD∽△N
1OB
1,
∴P
1为O N
1的中点.
∴

=

=

,
∴点P
1的坐标为(-

,-

).
将△P
1OD沿直线y=-x翻折,可得另一个满足条件的点到x轴距离等于P
1到y轴距离,点到y轴距离等于P
1到x轴距离,
∴此点坐标为:(

,

).
综上所述,点P的坐标为(-

,-

)和(

,

).
分析:(1)利用待定系数法求二次函数解析式进而得出答案即可;
(2)首先求出直线OB的解析式为y=x,进而将二次函数以一次函数联立求出交点即可;
(3)首先求出直线A′B的解析式,进而由△P
1OD∽△NOB,得出△P
1OD∽△N
1OB
1,进而求出点P
1的坐标,再利用翻折变换的性质得出另一点的坐标.
点评:此题主要考查了翻折变换的性质以及待定系数法求一次函数和二次函数解析式以及相似三角形的判定与性质等知识,利用翻折变换的性质得出对应点关系是解题关键.

 ,
, ,
,
 ,
, .
. x+3.
x+3. n+3),又点N在抛物线y=x2-3x上,
n+3),又点N在抛物线y=x2-3x上, n+3=n2-3n.
n+3=n2-3n. ,n2=4(不合题意,舍去),
,n2=4(不合题意,舍去), ,
,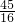 ).
).
 ,-
,- ),B1(4,-4).
),B1(4,-4). =
= =
= ,
, ,-
,- ).
). ,
, ).
). ,-
,- )和(
)和( ,
, ).
).

 名校课堂系列答案
名校课堂系列答案 下列说法:
下列说法:


