
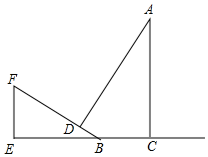
 如图,AC时一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,AC时一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光直射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树高AC的高度(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 分析 作DP⊥BE、DQ⊥AC,由∠DBP=30°、BD=4得CQ=DP=2、BP=2$\sqrt{3}$、DQ=BP+BC=2$\sqrt{3}$+6,由太阳光直射斜坡BF得∠ADQ=60°,从而求得AQ=DQtan∠ADQ=6+6$\sqrt{3}$,继而根据AC=AQ+CQ可得答案.
解答 解:如图,过点D作DP⊥BE于点P,作DQ⊥AC于点Q,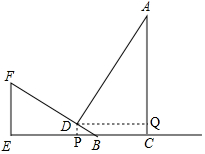
∵∠DBP=30°、BD=4,
∴CQ=DP=$\frac{1}{2}$BD=2,BP=BDcos∠DBP=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
则DQ=CP=BP+BC=2$\sqrt{3}$+6,
∵太阳光直射斜坡BF,
∴∠ADP=90°,
又∵∠QDB=∠DBP=30°,
∴∠ADQ=60°,
则AQ=DQtan∠ADQ=(2$\sqrt{3}$+6)$•\sqrt{3}$=6+6$\sqrt{3}$,
∴树高AC=AQ+CQ=6+6$\sqrt{3}$+2=8+6$\sqrt{3}$≈18.4(m),
答:树高AC的高度约为18.4m.
点评 本题主要考查解直角三角形的应用,题目中涉及到了仰俯角和坡度角的问题,解题的关键是构造直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
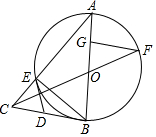 如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G.
如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
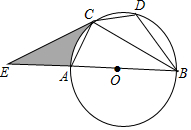 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,点D在⊙O上,AC=CD,延长BA到E,连接EC,且∠ECA=∠CBD.
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,点D在⊙O上,AC=CD,延长BA到E,连接EC,且∠ECA=∠CBD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
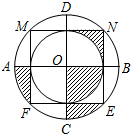 如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为$\frac{1}{4}$.
如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
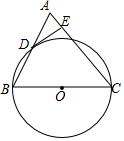 如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.
如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 95.32×106 | B. | 9.532×107 | C. | 9532×104 | D. | 0.9532×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{x+1}$ | B. | $\frac{2}{x-1}$ | C. | -$\frac{2}{x+1}$ | D. | -$\frac{2}{x-1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com