
【题目】七年级一班和二班各推选![]() 名同学进行投篮比赛,按照比赛规则,每人各投了
名同学进行投篮比赛,按照比赛规则,每人各投了![]() 个球,两个班选手的进球数统计如下表,请根据表中数据回答问题.
个球,两个班选手的进球数统计如下表,请根据表中数据回答问题.
进球数(个) |
|
|
|
|
|
|
一班人数(人) |
|
|
|
|
|
|
二班人数(人) |
|
|
|
|
|
|
![]() 填表;
填表;
平均数 | 中位数 | 众数 | 方差 | |
一班 | 2.6 | |||
二班 | 7 | 7 | 7 |
![]() 如果要从这两个班中选出一个班代表级部参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
如果要从这两个班中选出一个班代表级部参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用平均数、中位数和众数的定义直接求出;
(2)根据方差和个人发挥的最好成绩进行选择.
解:(1)一班进球平均数:![]() (10×1+9×1+8×1+7×4+6×0+5×3)=7(个),
(10×1+9×1+8×1+7×4+6×0+5×3)=7(个),
一班中位数:第五第六名同学进7个球,故中位数为7(个);
一班投中7个球的有4人,人数最多,故众数为7(个);
二班方差:S22=![]() [0×(10-7)2+(9-7)2+2×(8-7)2+5×(7-7)2+0×(6-7)2+2×(5-7)2]=1.4.
[0×(10-7)2+(9-7)2+2×(8-7)2+5×(7-7)2+0×(6-7)2+2×(5-7)2]=1.4.
(2)二班选手水平发挥更稳定,争取夺得总进球数团体第一名,应该选择二班;
一班前三名选手的成绩突出,分别进10个、9个、8个球,如果要争取个人进球数进入学校前三名,应该选择一班.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】以下是通过折叠正方形纸片得到等边三角形的步骤取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图,先把正方形ABCD对折,折痕为MN;
第二步:点E在线段MD上,将△ECD沿EC翻折,点D恰好落在MN上,记为点P,连接BP可得△BCP是等边三角形
问题:在折叠过程中,可以得到PB=PC;依据是________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
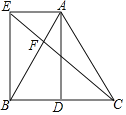
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若BE=2![]() ,AE=2,求EF的长.
,AE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师出示了这样一道题目:“当![]() 时,求多项式
时,求多项式![]() 的值”.解完这道题后,张恒同学指出:“
的值”.解完这道题后,张恒同学指出:“![]() 是多余的条件”师生讨论后,一致认为这种说法是正确的,老师及时给予表扬,同学们对张恒同学敢于提出自己的见解投去了赞赏的目光.
是多余的条件”师生讨论后,一致认为这种说法是正确的,老师及时给予表扬,同学们对张恒同学敢于提出自己的见解投去了赞赏的目光.
(1)请你说明正确的理由;
(2)受此启发,老师又出示了一道题目,“无论![]() 取任何值,多项式
取任何值,多项式![]() 的值都不变,求系数
的值都不变,求系数![]() 、
、![]() 的值”.请你解决这个问题.
的值”.请你解决这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个点从数轴上的原点开始,先向右移动1个单位长度,再向左移动2个单位长度,再向右移动3个单位长度,再向左移动4个单位长度,……,移动2019次后,该点所对应的数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
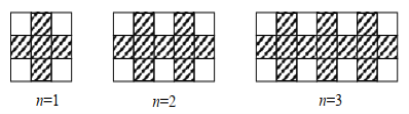
(1)铺第5个图形用黑色正方形瓷砖 块;
(2)按照此方式铺下去,铺第 n 个图形用黑色正方形瓷砖 块;(用含 n的代数式表示)
(3)若黑、白两种颜色的瓷砖规格都为( 长0.5米宽0.5米),且黑色正方形瓷砖每块价格 25 元,白色正方形瓷砖每块价格30元,若按照此方式恰好铺满该小路某一段(该段小路的总面积为 18.75 平方米),求该段小路所需瓷砖的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
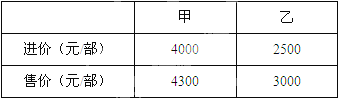
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2) 通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com