
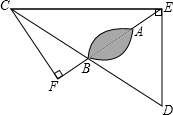
 (2013•梧州)海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D=
(2013•梧州)海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D=| 3 | 5 |
| DE |
| CD |
| 3 |
| 5 |
| 1 |
| 2 |
| BF |
| BC |
| 7 |
| 25 |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
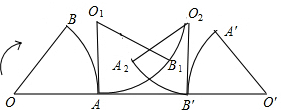 (2013•梧州模拟)如图,已知扇形的圆心角为60°,半径为1,将它沿着箭头方向无滑动滚动到O′A′B′位置,则有:
(2013•梧州模拟)如图,已知扇形的圆心角为60°,半径为1,将它沿着箭头方向无滑动滚动到O′A′B′位置,则有: |
| OO1 |
 |
| O1O2 |
 |
| O2O′ |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•梧州一模)某健身俱乐部有金牌会员、普通会员两种会员收费方式,其中金牌会员的消费额y(元)同月数x(个)之间符合图中的一次函数关系,普通会员按最低消费a元/月计算.
(2013•梧州一模)某健身俱乐部有金牌会员、普通会员两种会员收费方式,其中金牌会员的消费额y(元)同月数x(个)之间符合图中的一次函数关系,普通会员按最低消费a元/月计算.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com