
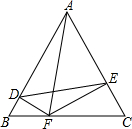
 △ABC是边长为4个单位长度的等边三角形,点F是边BC上的点,FD⊥AB,FE⊥AC,
△ABC是边长为4个单位长度的等边三角形,点F是边BC上的点,FD⊥AB,FE⊥AC,分析 (1)根据等边三角形的性质和垂直的定义结合两组对应角相等的两个三角形相似证明△BDF∽△CEF;
(2)根据A、D、F、E四点在同一个圆上,证明∠FAE=∠EDF,根据tan∠EDF=$\frac{\sqrt{3}}{2}$,设EF=$\sqrt{3}$x,根据∠ECF=60°和正切的概念列出算式求出x的值,得到答案.
(3)用m表示出AD、DF、AE、EF的长,根据四边形ADFE面积为S=△ADF的面积+△FEC的面积求出S与m之间的函数关系,根据配方法求出当m为何值时S取最大值.
解答 (1)证明:∵△ABC是等边三角形,
∴∠DBF=∠ECF=60°,
∵FD⊥AB,FE⊥AC,
∴∠BDF=∠CEF=90°,
∴:△BDF∽△CEF;
(2)解:∵A、D、F、E四点在同一个圆上,
∴∠FAE=∠EDF,
∴$\frac{EF}{AE}$=$\frac{\sqrt{3}}{2}$,
设EF=$\sqrt{3}$x,则AE=2x,由勾股定理得AF=$\sqrt{7}$x,
CE=4-2x,又∠ECF=60°,
tan∠ECF=$\frac{EF}{CE}$,即$\frac{\sqrt{3}x}{4-2x}$=$\sqrt{3}$,
解得x=$\frac{4}{3}$,
AF=$\sqrt{7}$x=$\frac{4}{3}\sqrt{7}$,
∵∠AEF=90°,
∴AF是圆的直径,
∴圆的半径为:$\frac{2}{3}\sqrt{7}$;
(3)解:在Rt△BDF中,∠B=60°,BF=m,
∴BD=$\frac{1}{2}$m,DF=$\frac{\sqrt{3}}{2}$m,
∴△ADF的面积为:$\frac{1}{2}$×(4-$\frac{1}{2}$m)×$\frac{\sqrt{3}}{2}$m=$\sqrt{3}$m-$\frac{\sqrt{3}}{8}$m2,
在Rt△FEC中,∠C=60°,FC=4-m,
∴EC=$\frac{1}{2}$(4-m),EF=$\frac{\sqrt{3}}{2}$(4-m),
∴△FEC的面积为:$\frac{1}{2}$×[4-$\frac{1}{2}$(4-m)]×$\frac{\sqrt{3}}{2}$(4-m)=2$\sqrt{3}$-$\frac{\sqrt{3}}{8}$m2,
四边形ADFE面积为S=△ADF的面积+△FEC的面积
=$\sqrt{3}$m-$\frac{\sqrt{3}}{8}$m2+2$\sqrt{3}$-$\frac{\sqrt{3}}{8}$m2,
=-$\frac{\sqrt{3}}{4}$(m-2)2+3$\sqrt{3}$,
当m=2时,S取最大值3$\sqrt{3}$.
点评 本题考查的是相似三角形的判定、四点共圆、锐角三角函数和二次函数的知识,掌握相似三角形的判定定理、锐角三角函数的概念和二次函数的最值的求法是解题的关键.


科目:初中数学 来源:2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
一个正方形的边长增加了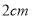 ,面积相应增加了
,面积相应增加了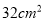 ,则这个正方形的边长为( )
,则这个正方形的边长为( )
A. 6cm B. 5cm C. 8cm D. 7cm
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
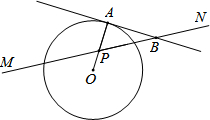 如图,⊙O的半径为2,点P是半径OA上的一个动点,过点P作直线MN且∠APN=60°,过点A的切线AB交MN于点B.设OP=x,△PAB的面积为 y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,⊙O的半径为2,点P是半径OA上的一个动点,过点P作直线MN且∠APN=60°,过点A的切线AB交MN于点B.设OP=x,△PAB的面积为 y,则下列图象中,能表示y与x的函数关系的图象大致是( )| A. |  | B. | 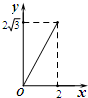 | C. |  | D. | 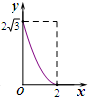 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
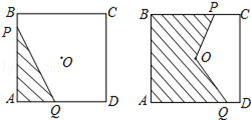 如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为y cm2,那么y与x的函数关系图象可能是( )
如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为y cm2,那么y与x的函数关系图象可能是( )| A. | 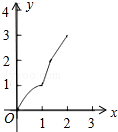 | B. | 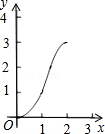 | C. | 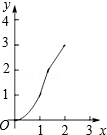 | D. | 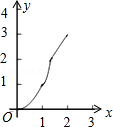 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售价格x(元/本) | … | 25 | 30 | 35 | 40 | … |
| 销售量y(本) | … | 250 | 200 | 150 | 100 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com