
【题目】如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
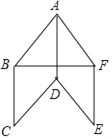
【答案】(1)证明见解析;(2)150°
【解析】试题分析:(1)连结DB、DF.根据菱形四边相等得出AB=AD=FA,再利用SAS证明△BAD≌△FAD,得出DB=DF,那么D在线段BF的垂直平分线上,又AB=AF,即A在线段BF的垂直平分线上,进而证明AD⊥BF;
(2)设AD⊥BF于H,作DG⊥BC于G,证明DG=![]() CD.在直角△CDG中得出∠C=30°,再根据平行线的性质即可求出∠ADC=180°﹣∠C=150°.
CD.在直角△CDG中得出∠C=30°,再根据平行线的性质即可求出∠ADC=180°﹣∠C=150°.
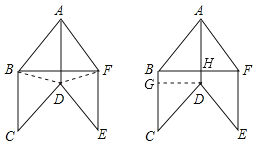
(1)证明:如图,连结DB、DF.
∵四边形ABCD,ADEF都是菱形,∴AB=BC=CD=DA,AD=DE=EF=FA.
在△BAD与△FAD中,∵AB=AF,∠BAD=∠FAD,AD=AD,∴△BAD≌△FAD,∴DB=DF,∴D在线段BF的垂直平分线上,∵AB=AF,∴A在线段BF的垂直平分线上,∴AD是线段BF的垂直平分线,∴AD⊥BF;
(2)如图,设AD⊥BF于H,作DG⊥BC于G,则四边形BGDH是矩形,∴DG=BH=![]() BF.∵BF=BC,BC=CD,∴DG=
BF.∵BF=BC,BC=CD,∴DG=![]() CD.在直角△CDG中,∵∠CGD=90°,DG=
CD.在直角△CDG中,∵∠CGD=90°,DG=![]() CD,∴∠C=30°,∵BC∥AD,∴∠ADC=180°﹣∠C=150°.
CD,∴∠C=30°,∵BC∥AD,∴∠ADC=180°﹣∠C=150°.


科目:初中数学 来源: 题型:
【题目】如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今年考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是 ,破译“正做数学”的真实意思是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB与直线CD相交于点O,OE平分![]() .
.
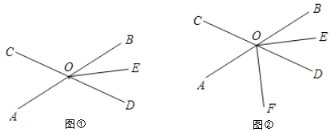
(1)如图①,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,射线OF在![]() 内部.
内部.
①若![]() ,判断OF是否为
,判断OF是否为![]() 的平分线,并说明理由;
的平分线,并说明理由;
②若OF平分![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线 y=x+2 与两坐标轴分别交于A、B 两点,点 C 是 OB 的中点,D、E 分 别是直线 AB、y 轴上的动点,则△CDE 周长的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
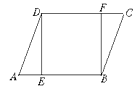
【题目】如图,在平行四边ABCD中,E、F分别是AB、DC上的点,且AE=CF,
(1)求证:△ADE≌△CBF;
(2) 当∠DEB=90°时,试说明四边形DEBF为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() (x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=
(x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE= ![]() CB,AF=
CB,AF= ![]() AB,且四边形OEBF的面积为2,则k的值为 .
AB,且四边形OEBF的面积为2,则k的值为 . 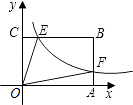
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴和y轴上,OA=3,OB=4.把△AOB绕点A顺时针旋转120°,得到△ADC.边OB上的一点M旋转后的对应点为M′,当AM′+DM取得最小值时,点M的坐标为( )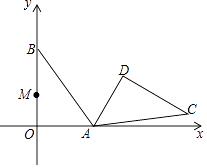
A.(0, ![]() )
)
B.(0, ![]() )
)
C.(0, ![]() )
)
D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人分别驾车从![]() 同时出发,沿同一条线路相向而行,甲从
同时出发,沿同一条线路相向而行,甲从![]() 地以速度52km/h匀速去
地以速度52km/h匀速去![]() 地,乙开始以速度
地,乙开始以速度![]() km/h匀速行驶,中途速度改为
km/h匀速行驶,中途速度改为![]() km/h匀速行驶,到
km/h匀速行驶,到![]() 恰好用时
恰好用时![]() ,两人距离
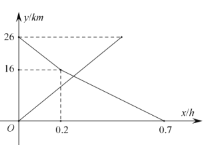
,两人距离![]() 地的路程与各自离开出发地的时间之间的图象如图所示.求:
地的路程与各自离开出发地的时间之间的图象如图所示.求:
(1)![]() 两地之间的路程为多少
两地之间的路程为多少![]() 及乙开始的速度
及乙开始的速度![]() ;
;
(2)当两人相距![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com