
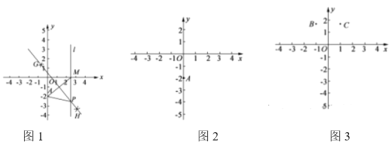
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A��������![]() ����x������ȡһ��M������AM���ֱ��Ե�A�͵�MΪԲ�ģ�����
����x������ȡһ��M������AM���ֱ��Ե�A�͵�MΪԲ�ģ�����![]() �ij�Ϊ�뾶�����������ཻ��G��H���㣬��ֱ��GH������M��x��Ĵ���l��ֱ��GH�ڵ�P���������ϲ���������������⣮
�ij�Ϊ�뾶�����������ཻ��G��H���㣬��ֱ��GH������M��x��Ĵ���l��ֱ��GH�ڵ�P���������ϲ���������������⣮
̽����
��1���߶�PA��PM��������ϵΪ________��������Ϊ��________________��
��2����x���϶�θı��M��λ�ã���������ͼ�����õ���Ӧ��P�����꣬��������б���
M������ | �� |
|
|
|
| �� |
P������ | �� |
|
| �� |
���룺
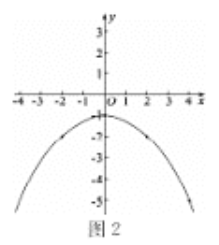
��3�����������������P������꣬����Щ����ƽ����������ͼ2�������������۲컭��������L����������L����״��________��
��֤��
��4�����P��������![]() ������ͼ1���߶�PA��PM�Ĺ�ϵ�����y����x�ĺ�������ʽ��
������ͼ1���߶�PA��PM�Ĺ�ϵ�����y����x�ĺ�������ʽ��
Ӧ�ã�
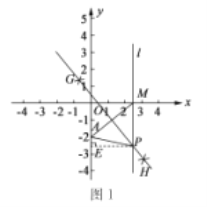
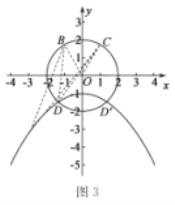
��5����ͼ3����![]() ��
��![]() �����D��������
�����D��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��![]() ���߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ�����ȣ���2��ͼ�������������ߣ���3������������4��
���߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ�����ȣ���2��ͼ�������������ߣ���3������������4��![]() ����5��
����5��![]()
��������
��1���ɳ߹���ͼ�IJ����֪��HG��AM���д��ߣ�����д��ߵ����ʣ����ɵõ��𰸣�
��2�����ݵڣ�1������ͼ�������õ���Ӧ��P��λ�ã�������⣻
��3����ƽ������������ͼ���ɣ�
��4������P��![]() ���ڵ�E���ú�x��y�Ĵ���ʽ��ʾ
���ڵ�E���ú�x��y�Ĵ���ʽ��ʾ![]() ��
��![]() ��
��![]() ����Ϲ��ɶ��������ɵõ��𰸣�
����Ϲ��ɶ��������ɵõ��𰸣�
��5������![]() ��������õ�
��������õ�![]() ʱ����
ʱ����![]() �����Բ�ϣ���
�����Բ�ϣ���![]() ���Ե�Բ�Ľ�Ϊ60�㣬
���Ե�Բ�Ľ�Ϊ60�㣬![]() �����ԲԲ��Ϊ����ԭ��O����
�����ԲԲ��Ϊ����ԭ��O����![]() �����b��ֵ������������⣮
�����b��ֵ������������⣮
�⣺��1��![]() �߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ������
�߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ������
��2��
M������ | �� |
|
|
|
| �� |
P������ | �� |
|
|
|
| �� |
��3����ͼ��ͼ2����״��������
��4����ͼ1������P��![]() ���ڵ�E��
���ڵ�E��
![]() ��
��![]() ��
��![]()
��![]() ��
�У�![]()
��![]()
����![]()
��y����x�ĺ�������ʽΪ![]() ��
��
��5������![]() ����
����![]() ����
����![]()
��![]() Ϊ�ȱ������Σ���
Ϊ�ȱ������Σ���![]()
��![]() ʱ����
ʱ����![]() �����Բ�ϣ���
�����Բ�ϣ���![]() ���Ե�Բ�Ľ�Ϊ60��
���Ե�Բ�Ľ�Ϊ60��
��Բ����![]() �Ĵ�ֱƽ����y���ϣ�
�Ĵ�ֱƽ����y���ϣ�
��![]() �����ԲԲ��Ϊ����ԭ��O��
�����ԲԲ��Ϊ����ԭ��O��
��![]() ����
����![]() ����
����![]() ��
��
�ֵ�D�ڸ���������
��![]() ��
��
�ɢ٢�������ã�![]() ����ȥ��
����ȥ��
���ν�Ͽɵã�
��![]() ʱ����D��������
ʱ����D��������![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ
![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������֮����һ��ֱ·����ȫ������У��������ܲ��Ӽ����ҵأ������������г����ҵ����أ�����ͬʱ�������������ȵ���Ŀ�ĵأ�����֮��ľ���![]() ���˶�ʱ��
���˶�ʱ��![]() �ĺ�����ϵ������ͼ��ʾ������˵���д�����ǣ� ����
�ĺ�����ϵ������ͼ��ʾ������˵���д�����ǣ� ����
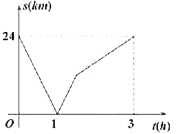
A.���˳���1Сʱ������B.�������ܲ����ٶ�Ϊ![]()
C.�����µ���Ŀ�ĵ�ʱ�������![]() D.�����±���������ǰ
D.�����±���������ǰ![]() ��Ŀ�ĵ�
��Ŀ�ĵ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=3��BC=4������P��A���������A��B��C�ķ�����AB��BC���ƶ�����PA=x����D��ֱ��PA�ľ���Ϊy����y����x�ĺ���ͼ������ǣ� ��

A. B.
B.
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����²��ϣ��������Ӧ���⣺
С���ڿ���ѧϰʱ��������һ�����⣺
���壺������κ���y��a1x2+b1x+c1��a1��0��a1��b1��c1�dz�������y��a2x2+b2x+c2��a2��0��a2��b2��c2�dz���������a1+a2��0��b1��b2��c1+c2��0����������������Ϊ����ת������������y��2x2��3x+1����ת������С��������˼���ģ��ɺ���y��2x2��3x+1��֪��a1��2��b1����3��c1��1������a1+a2��0��b1��b2��c1+c2��0�����a2��b2��c2����ȷ�������������ת������
��˼��С���ķ�������������⣺
��1��д������y��x2��4x+3����ת������
��2��������y��5x2+��m��1��x+n��y����5x2��nx��3��Ϊ��ת��������m+n��2020��ֵ��
��3����֪����y��2��x��1����x+3����ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����A��B��C����ԭ��ĶԳƵ�ֱ���A1��B1��C1������֤��������A1��B1��C1�Ķ��κ�����y��2��x��1����x+3����Ϊ����ת��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
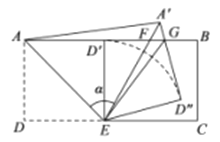
����Ŀ����ͼ���ھ���ABCD�У�![]() ��
��![]() ������EAD��AE�۵���ʹ��Dǡ������AB���ϵ�
������EAD��AE�۵���ʹ��Dǡ������AB���ϵ�![]() �����ٽ�
�����ٽ�![]() �Ƶ�E˳ʱ����ת
�Ƶ�E˳ʱ����ת![]() ���õ�
���õ�![]() ��ʹ��
��ʹ��![]() ǡ�þ���
ǡ�þ���![]() ���е�F��
���е�F��![]() ��AB�ڵ�G������
��AB�ڵ�G������![]() �����½��ۣ���
�����½��ۣ���![]() �ij�����
�ij�����![]() ���ڻ�
���ڻ�![]() �ij�����
�ij�����![]() ����
����![]() ����
����![]() �����������У�������ȷ�������________��
�����������У�������ȷ�������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �����������
�����������![]() ��
��

��1������ͼ1�����̶ȵ�ֱ�ߺ�Բ����ͼ����ֱ��![]() ��ʹ
��ʹ![]() �ϵĸ��㵽
�ϵĸ��㵽![]() ��
��![]() ����ľ�����ȣ���ֱ��
����ľ�����ȣ���ֱ��![]() ��
��![]() ��
��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ����һ��Բ��ʹ��Բ��
����һ��Բ��ʹ��Բ��![]() ���߶�
���߶�![]() �ϣ������
�ϣ������![]() ��
��![]() ���У�����д������������ͼ�ۼ���
���У�����д������������ͼ�ۼ���
��2���ڣ�1���������£���![]() ��
��![]() ����
����![]() �İ뾶Ϊ________��
�İ뾶Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O��AB�ǡ�O��ֱ������P��CA���ӳ����ϣ���CAD=45��.

(1)��AB=4����CD�ij�.
(2)����BC=��AD��AD=AP. ��֤��PD�ǡ�O������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У�![]() ,��ACΪֱ���İ�ԲO���ڵ�D������D��ԲO�����ߣ���BC�ڵ�E����F�ǰ�Բ�����ڵ�D����һ���㣮
,��ACΪֱ���İ�ԲO���ڵ�D������D��ԲO�����ߣ���BC�ڵ�E����F�ǰ�Բ�����ڵ�D����һ���㣮
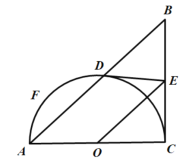
��1����֤��![]() ��
��
��2����գ�
����![]() �����ı���
�����ı���![]() �����Ϊ________��
�����Ϊ________��
�ڵ�![]() �Ķ�����_______ʱ����
�Ķ�����_______ʱ����![]() Ϊ������ı���Ϊ���Σ�
Ϊ������ı���Ϊ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ҵ������̳ǵ��������ۼ�Ϊÿ̨2100Ԫ���յ������ۼ�Ϊÿ̨1750Ԫ��ÿ̨�����Ľ��۱�ÿ̨�յ��Ľ��۶�400Ԫ���̳���80000Ԫ������������������64000Ԫ�����յ���������ȣ�
��ÿ̨�������յ��Ľ��۷ֱ��Ƕ��٣�
��2�������̳���һ�ι��������ּҵ繲100̨���蹺�������x̨����100̨�ҵ������������ΪyԪ��Ҫ���յ����������������������2������������13000Ԫ������������ķ������ж����֣���ȷ���������ķ����Լ��������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com