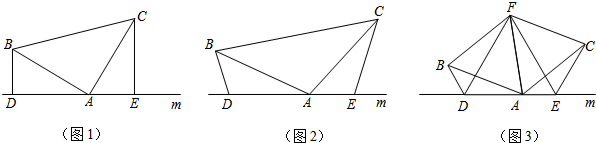
证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中

,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中

,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)由(2)知,△ADB≌△CEA,
BD=AE,∠DBA=∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
∵BF=AF
在△DBF和△EAF中

,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
分析:(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,
则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
(2)与(1)的证明方法一样;
(3)与前面的结论得到△ADB≌△CEA,则BD=AE,∠DBA=∠CAE,根据等边三角形的性质得∠ABF=∠CAF=60°,则∠DBA+∠ABF=∠CAE+∠CAF,则∠DBF=∠FAE,
利用“SAS”可判断△DBF≌△EAF,所以DF=EF,∠BFD=∠AFE,于是∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,根据等边三角形的判定方法可得到△DEF为等边三角形.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.

 ,
, ,
, ,
,

 名校课堂系列答案
名校课堂系列答案

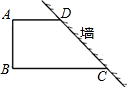 ,设AB=AD=x米,BC=y米,且x<y.
,设AB=AD=x米,BC=y米,且x<y.