
����Ŀ����ͼ1,��ƽ��ֱ������ϵ��,A��a,0����x����������һ��,C�ǵ�������һ��,CB��y��,��y�Ḻ������B��0,b��,��(a-3)2+|b+4|=0,S�ı���AOBC=16��
��1����C�����ꣻ
��2����ͼ2,��DΪ�߶�OB��һ����,��AD��ACʱ,��ODA�Ľ�ƽ�������CAE�Ľ�ƽ���ߵķ����ӳ��߽��ڵ�P,���APD�Ķ�����
��3����ͼ3,��D�����߶�OB���˶�ʱ,��DM��AD��BC��M��,��BMD����DAO��ƽ���߽���N��,��D�����˶�������,��N�Ĵ�С�Ƿ�仯��������,�����ֵ,���仯,˵�����ɣ�
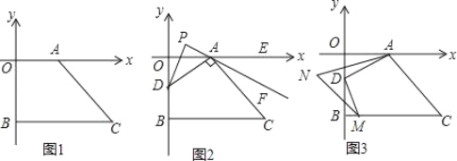
���𰸡�(1) C��5����4��;(2)90��;(3)������.
����������1�����÷Ǹ����ĺ�Ϊ�㣬����ֱ�Ϊ�㣬���a��b���ɣ�
��2����ͬ�ǵ������Ⱥͽ�ƽ���ߵ����弴�ɣ�
��3�����ý�ƽ���ߵ�����ͻ������ǵĹ�ϵ����֤�����ɣ�
��1������a��3��2+|b+4|=0��
��a��3=0��b+4=0��
��a=3��b=��4��
��A��3��0����B��0����4����
��OA=3��OB=4��
��S�ı���AOBC=16��
��0.5��OA+BC����OB=16��
��0.5��3+BC����4=16��
��BC=5��
��C�ǵ�������һ�㣬CB��y�ᣬ
��C��5����4����
��2����ͼ��

�ӳ�CA����AF�ǡ�CAE�Ľ�ƽ���ߣ�
���CAF=0.5��CAE��
�ߡ�CAE=��OAG��
���CAF=0.5��OAG��
��AD��AC��
���DAO+��OAG=��PAD+��PAG=90�㣬
�ߡ�AOD=90�㣬
���DAO+��ADO=90�㣬
���ADO=��OAG��
���CAF=0.5��ADO��
��DP�ǡ�ODA�Ľ�ƽ������
���ADO=2��ADP��
���CAF=��ADP��
�ߡ�CAF=��PAG��
���PAG=��ADP��
���APD=180�㩁����ADP+��PAD��=180�㩁����PAG+��PAD��=180�㩁90��=90��
������APD=90��
��3�����䣬��ANM=45�����ɣ���ͼ��

�ߡ�AOD=90�㣬
���ADO+��DAO=90�㣬
��DM��AD��
���ADO+��BDM=90�㣬
���DAO=��BDM��
��NA�ǡ�OAD��ƽ���ߣ�
���DAN=0.5��DAO=0.5��BDM��
��CB��y�ᣬ
���BDM+��BMD=90�㣬
���DAN=0.5��90�㩁��BMD����
��MN�ǡ�BMD�Ľ�ƽ���ߣ�
���DMN=0.5��BMD��
���DAN+��DMN=0.5��90�㩁��BMD��+0.5��BMD=45��
����DAM�У���ADM=90�㣬
���DAM+��DMA=90�㣬
����AMN��
��ANM=180�㩁����NAM+��NMA��=180�㩁����DAN+��DAM+��DMN+��DMA��=180�㩁[����DAN+DMN��+����DAM+��DMA��] =180�㩁��45��+90�㣩=45�㣬
��D�����˶������У���N�Ĵ�С���䣬�����ֵΪ45��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��DB����ABD��ƽ����BE��AD�ڵ�E����CDB��ƽ����DF��BC�ڵ�F����֤���ı���DFBE�Ǿ��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ ABCD �ĶԽ��� AC �� BD �ཻ�ڵ� O,CE��BD, DE��AC , AD��2![]() , DE��2,���ı��� OCED �����Ϊ��������
, DE��2,���ı��� OCED �����Ϊ��������

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=�� ![]() x+3��������ֱ��ڵ�A��B����P��������y=��
x+3��������ֱ��ڵ�A��B����P��������y=�� ![]() ��x��
��x�� ![]() ��2+4�ϣ���ʹ��ABPΪ���������εĵ�P�ĸ����У�������
��2+4�ϣ���ʹ��ABPΪ���������εĵ�P�ĸ����У�������
A.3��
B.4��
C.5��
D.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��
��1����֤��OE=OF��
��2����CE=12��CF=5����OC�ij���
��3������O�ڱ�AC���˶���ʲôλ��ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�
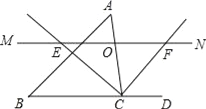
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵķ�ʽƴ��һ��������.
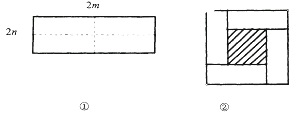
(1)����Ϊͼ���е���Ӱ���ֵ������εı߳�����_________________.
(2)�������ֲ�ͬ�ķ����д���ʽ��ʾͼ������Ӱ���ֵ����.
������_________________________________________________________.
������_________________________________________________________.
(3)�۲�ͼ�ڣ�����д��(m+n)2��(m-n)2��mn����������ʽ��ĵ�����ϵ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��DF����D+��B=180����

��1����֤��DE��BC��
��2�������AMD=75�������AGC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���жԽ�����Ϊ10Ԫ/ǧ�˵�ij��ƻ���������������ͳ�ƣ�����ÿ��������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ�����һ�κ�����ϵ����ͼ��ʾ�� 
��1����y����x�ĺ�����ϵʽ����Ҫ��д��x��ȡֵ��Χ����
��2��Ӧ����ȷ�����ۼۣ�ʹ��Ʒ��ƻ����ÿ���������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ�Ӫ����Сѧ�������蹤���У�ijѧУ�ƻ�����һ�����Ժ͵��Ӱװ壬�����г������֪������1̨���Ժ�2̨���Ӱװ���Ҫ3.5��Ԫ������2̨���Ժ�1̨���Ӱװ���Ҫ2.5��Ԫ.
��1����ÿ̨���ԡ�ÿ̨���Ӱװ��������Ԫ?
��2������ѧУʵ�ʣ��蹺�����Ժ͵��Ӱװ干30̨���ܷ��ò�����30��Ԫ����������28��Ԫ������ͨ����������м��ֹ��������ַ����������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com