
����Ŀ����ͼ����������AM��BN���߶�CD�������˵�C��D�ֱ�������BN��AM�ϣ��ҡ�A����BCD��108�㣮E���߶�AD��һ�㣨�����A��D�غϣ�����BDƽ�֡�EBC��
��1�����ABC�Ķ�����
��2������ͼ���ҳ����ABC��ȵĽǣ���˵�����ɣ�
��3����ƽ���ƶ�CD����AD��CD�����ADB���AEB�Ķ���֮���Ƿ�����CDλ�õı仯�������仯�����仯���ҳ��仯���ɣ������䣬��������ֵ��

���𰸡���1����ABC=72�㣻��2������ABC��ȵĽ�����ADC����DCN����3���������仯����ֵΪ![]() .
.
��������
��1����ƽ���ߵ����ʿ���á�A+��ABC��180�㣬������ô���
��2������ƽ���ߵ����ʿ���á�ADC����DCN����ADC+��BCD��180�㣬�����ô���
��3������ƽ���ߵ�����������á�AEB����EBC����ADB����DBC���ٽ�Ͻ�ƽ���ߵĶ������ô���
��1����AM��BN�����A+��ABC��180�㣬���ABC��180�㩁��A��180�㩁108�㣽72�㣮
��2�����ABC��ȵĽ��ǡ�ADC����DCN��
��AM��BN�����ADC����DCN����ADC+��BCD��180�㣬���ADC��180�㩁��BCD��180�㩁108�㣽72�㣬���DCN��72�㣬���ADC����DCN����ABC��
��3���������仯��
��AM��BN�����AEB����EBC����ADB����DBC��
��BDƽ�֡�EBC�����DBC![]() ��EBC�����ADB
��EBC�����ADB![]() ��AEB�����
��AEB�����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪������OABC��A(4��0)��C(0��4)������P�ӵ�A��������ABCO��·�������˶����趯��P���˶�·��Ϊt����OAP�����ΪS���������ܴ��·�ӳS��t֮���ϵ��ͼ����(����)
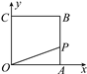

A. ��A�� B. ��B�� C. ��C�� D. ��D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,��֪��AOB��һ�������߶�a,����AOB����һ��P,ʹ��P��OA,OB�ľ��붼����a,��������:
������AOB����OB�Ĵ��߶�NH,ʹNH=a,HΪ����;�ڹ�N��NM��OB;������AOB��ƽ����OP,��NM���ڵ�P;�ܵ�P��Ϊ����.���Т۵�������(����)

A. ƽ����֮��ľ��봦����� B. �ǵ��ڲ����ǵ����ߵľ�����ȵĵ��ڽǵ�ƽ������
C. �ǵ�ƽ�����ϵĵ㵽�ǵ����ߵľ������ D. �߶δ�ֱƽ�����ϵĵ㵽�߶����˵�ľ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC��,AB=AC,ADƽ�֡�BAC,DE��AB��E��,DF��AC��F��,�����н���:��BD=DC;��DE=DF;��AD������һ�㵽AB,AC�ľ������;��AD������һ�㵽B����C��ľ��벻��.������ȷ����(����)

A. �٢� B. �ۢ� C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����5�֣�ij���г���һ�ܼƻ�����1400�����г���ƽ��ÿ������200�������ڸ���ԭ��ʵ��ÿ����������ƻ�������г��룬�±���ij�ܵ��������������Ϊ��������Ϊ������

�Ÿ��ݼ�¼��֪ǰ���칲����________����
�Ʋ�������һ��Ȳ������ٵ�һ�������________����
�Ǹó�ʵ�мƼ������ƣ�ÿ����60Ԫ�������������ÿ����15Ԫ��������һ����15Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��a��b��c��ʾ������·����Ҫ��һ��������תվ��Ҫ������������·�ľ�����ȣ���ɹ�ѡ��ĵ�ַ��_______��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ��
��![]() ��
��![]() ��
��![]() ����һ����Ϊ2016����λ������û�е��Ե�ϸ��
����һ����Ϊ2016����λ������û�е��Ե�ϸ��![]() �ߵĴ�ϸ���Բ���
�ߵĴ�ϸ���Բ���![]() ��һ�˹̶��ڵ�A��������
��һ�˹̶��ڵ�A��������![]() �Ĺ��������ı���ABCD�ı��ϣ���ϸ����һ������λ�õĵ��������
�Ĺ��������ı���ABCD�ı��ϣ���ϸ����һ������λ�õĵ��������![]() ����
����![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����ٽ�����⣬���⣺��m2+2mn+2n2��6n+9=0����m��n��ֵ.
�⣺��m2+2mn+2n2��6n+9=0
��(m+n)2+(n��3)2=0
��m+n=0��n��3=0
��n=3��m=��3
(1)��x2+2y2��2xy+4y+4=0����xy��ֵ
(2)��֪��ABC�����߳�a��b��c������������������a2+b2��6a��6b+18+|3��c|=0�����ʡ�ABC��������״�������Σ�
(3)�������ϵķ�����˵������ʽ��x2+4x+y2��8y+21��ֵһ����һ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڰ˴���ѧ�����У��ס������˵ijɼ����£�
�ף�89��93��88��91��94��90��88��87 �ң�92��90��85��93��95��86��87��92
��������нǶȱȽ����˳ɼ����������˵�����ɣ�
��1���ֱ�������˵ļ����˵��˭�ijɼ��仯��Χ��
��2������ƽ�������ж����˵ijɼ�˭��˭�Σ�
��3�������������ж����˵ijɼ�˭��˭�Σ�
��4��������λ�����ж����˵ijɼ�˭��˭�Σ�
��5�����ݷ������ж����˵ijɼ�˭���ȶ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com