
【题目】如图,在平面直角坐标系中,已知点A(5,0)和点B(0,4).


(1)求直线AB所对应的函数表达式;
(2)设直线y=x与直线AB相交于点C,求△BOC的面积;
(3)若将直线OC沿x轴向右平移,交y轴于点O′,当△AB O′为等腰三角形时,直接写出点O′的坐标.
【答案】(1)![]() ; (2)S△BOC=
; (2)S△BOC=![]() ;(3) 点O′的坐标为(0,
;(3) 点O′的坐标为(0,![]() )或(0,-4)或(0,
)或(0,-4)或(0,![]() ).
).
【解析】
(1)根据点A,B的坐标,利用待定系数法即可求出直线AB所对应的函数表达式;
(2)联立直线OC及直线AB所对应的函数表达式为方程组,通过解方程组可求出点C的坐标,再利用三角形的面积公式结合点B的坐标即可求出△BOC的面积;
(3)分AB=AO′,O′B=O′A,BA=BO′三种情况考虑:①当AB=AO′时,由等腰三角形的性质可得出OB=OO′,结合点B的坐标可得出点O′的坐标;②当O′B=O′A时,设OO′=x,则O′A=4+x,在Rt△AOO′中利用勾股定理可求出x的值,进而可得出点O′的坐标;③当BA=BO′时,利用勾股定理可求出BO′的值,结合点B的坐标可得出点O′的坐标.综上,此题得解.
解:(1)∵A(5,0),B(0,4)
设AB表达式为:y=kx+b,将A,B坐标代入表达式![]() ,
,
解得:k=![]() ,b=4,
,b=4,
∴AB表达式为:![]() .
.
(2) 联立![]() 和y=x,
和y=x,
解得:y=x=![]()
∴C(![]() ,
,![]() ),
),
∴S△BOC=![]() =
=![]() .
.
(3) 若△ABO′为等腰三角形,有三种情况
①当AB=AO时,由三线合一可得OB=OO′,
∵B(0,4),
∴O′(0,-4);
②当O′B=O′A时,设OO′=x,
∴O′B=O′A=4+x,
∵OA=5,
∴在△OO′A中,OO′2+OA2=O′A2,
则x2+52=(4+x)2,
解得:x=![]() ,
,
∴O′(0,![]() );
);
③当BA=BO′时,设OO′=y,
∴O′B=AB=4+y,
∵OA=5,
∴在△ABO中,AO2+BO2=AB2,
则42+52=(4+y)2,
解得:y=![]() ,
,
∴O′(0,![]() )
)
综上:点O′的坐标为(0,![]() )或(0,-4)或(0,
)或(0,-4)或(0,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,小华同学想测量学校逸夫楼的高度,他站在B点从A处仰望楼顶D,测得仰角为30°,再往逸夫楼的方向前进14米从E处望楼顶,测得仰角为60°,已知小华同学身高(AB)为1.6米,则逸夫楼CD的高度的为( )(![]() ≈1.73)
≈1.73)

A.12.1米B.13.7米C.11.5米D.13.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
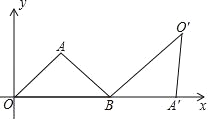
【题目】如图,点A的坐标为(3,![]() ),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为_____.
),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
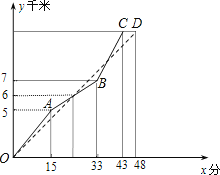
【题目】如图表示甲、乙两名选手在一次自行车越野赛中,路程y(千米)随时间x(分)变化的图象.下面几个结论:①比赛开始24分钟时,两人第一次相遇.②这次比赛全程是10千米.③比赛开始38分钟时,两人第二次相遇.正确的结论为_____(只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,∠A=36°.

(1)尺规作图:作AB的垂直平分线MN交AC于点D,连接BD;(保留作图痕迹,不写作法)
(2)求∠DBC的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线M:y=ax2+bx+c(a≠0)经过A(﹣1,0),且顶点坐标为B(0,1).
(1)求抛物线M的函数表达式;
(2)设F(t,0)为x轴正半轴上一点,将抛物线M绕点F旋转180°得到抛物线M1.
①抛物线M1的顶点B1的坐标为 ;
②当抛物线M1与线段AB有公共点时,结合函数的图象,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
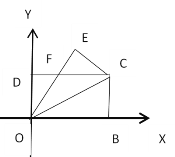
【题目】如图,长方形OBCD的OB边在x轴上,OD在y轴上,把OBC沿OC折叠得到OCE,OE与CD交于点F.
(1)求证:OF=CF;
(2)若OD=4,OB=8,写出OE所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于国家对农业的大力扶持,农民的种粮积极性得到极大提高.国家统计局提供的数据表明,我国粮食产量连续两年大幅增长,![]() 年粮食产量为
年粮食产量为![]() 亿斤,
亿斤,![]() 年达到了
年达到了![]() 亿斤,若要求这两年粮食产量的平均增长率,可设平均增长率为
亿斤,若要求这两年粮食产量的平均增长率,可设平均增长率为![]() ,列方程为________.
,列方程为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com