
分析 根据题意可以画出相应的图形,然后根据不同情况,求出相应的边的长度,从而可以求出不同情况下△ABC的面积.
解答 解:由题意可得,
当△ABC为△A1BC时,连接OB、OC,
∵点O是等腰△ABC的外心,且∠BOC=60°,底边BC=4,OB=OC,
∴△OBC为等边三角形,OB=OC=BC=4,OA1⊥BC于点D,
∴CD=2,
∴OD=$\sqrt{O{C}^{2}-C{D}^{2}}$=2$\sqrt{3}$,
∴A1D=4-2$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$×4×(4-2$\sqrt{3}$)=8-4$\sqrt{3}$,
当△ABC为△A2BC时,连接OB、OC,
A2D=4+2$\sqrt{3}$
同理可得,△ABC的面积=8+4$\sqrt{3}$,
故答案为:8-4$\sqrt{3}$或8+4$\sqrt{3}$.
点评 本题考查三角形的外接圆和外心,等腰三角形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答问题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
| 累计购物 | 130 | 250 | … |
| 在甲商场 实际花费 | 100+(130-100)×90% | 100+(250-100)×90% | … |
| 在乙商场 实际花费 | 50+(130-50)×95% | 50+(250-50)×95% | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18(42-x)=12x | B. | 2×18(42-x)=12x | C. | 18(42-x)=2×12x | D. | 18(21-x)=12x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
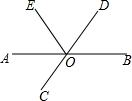 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com