
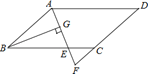
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=![]() ,则△CEF的面积是( )
,则△CEF的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
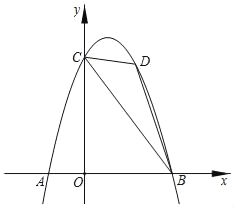
【题目】如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(1<m<4)连接BC,DB,DC.
(1)求抛物线的函数解析式;
(2)△BCD的面积是否存在最大值,若存在,求此时点D的坐标;若不存在,说明理由;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我省部分地区遭遇严重干旱,为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系.
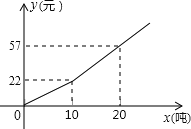
(1)小聪家五月份用水7吨,应交水费 元;
(2)按上述分段收费标准,小聪家三、四月份分别交水费29元和19.8元,问四月份比三月份节约用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并解答问题:杨辉和他的一个数学问题:提起代数,人们自然就和方程联系起米.事实上,我国古代对代数的研究,特别是对方程的解法研究有着优良的传统并取得了重要成果.杨辉,字谦光,钱塘(今浙江杭州)人,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著述,他著名的数学书共五种二十一卷.下面是杨辉在1275年提出的一个问题(选自杨辉所著《田亩比类乘除算法》):直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.请你用学过的知识解决这个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在反比例函数![]() 的图象上的概率;
的图象上的概率;
(3)求小明、小华各取一次小球所确定的数x、y满足![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,双曲线
,双曲线![]()
![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,且与
,且与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
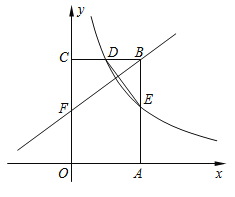
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)若点![]() 是
是![]() 边上一点,且
边上一点,且![]() 相似于
相似于![]() .求直线
.求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(a,y1),Q(1,y2)是抛物线y=kx2+(2k+1)x+2(k是不等于0的常数)上的两点.
(1)求证:无论k取任何实数时,关于x的方程kx2+(2k+1)x+2=0总有实数根;
(2)当k=1时,
①求抛物线y=kx2+(2k+1)x+2图象与x轴两个交点坐标,并画出此条抛物线的草图;
②若y1>y2,请结合函数图象确定实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①abc<0;②4a+2b+c>0;③5a﹣b+c=0;④若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1;⑤若方程|ax2+bx+c|=1有四个根,则这四个根的和为﹣8,其中正确的结论有( )
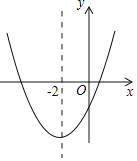
A.①②③④B.①②③⑤C.②③④⑤D.①②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.25人中至少有3人的出生月份相同
B.任意抛掷一枚均匀的1元硬币,若上一次正面朝上,则下一次一定反面朝上
C.天气预报说明天降雨的概率为10%,则明天一定是晴天
D.任意抛掷一枚均匀的骰子,掷出的点数小于3的概率是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com