
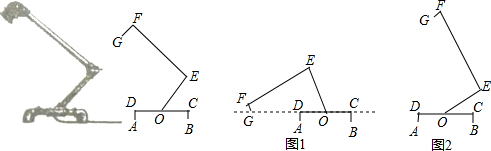
分析 (1)作GM⊥OE可得矩形EFGM,设FG=xcm,可知EF=GM=20$\sqrt{3}$cm,OM=(20-x)cm,根据tan∠EOG=$\frac{GM}{OM}$列方程可求得x的值;
(2)RT△EFO中求出OF的长及∠EOF的度数,由∠EOG度数可得旋转角∠FOF′度数,根据弧长公式计算可得.
解答 解:(1)如图,作GM⊥OE于点M,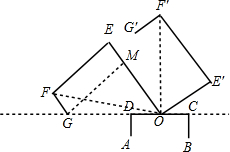
∵FE⊥OE,GF⊥EF,
∴四边形EFGM为矩形,
设FG=xcm,
∴EF=GM=20$\sqrt{3}$cm,FG=EM=xcm,
∵OE=20cm,
∴OM=(20-x)cm,
在RT△OGM中,
∵∠EOG=65°,
∴tan∠EOG=$\frac{GM}{OM}$,即$\frac{20\sqrt{3}}{20-x}$=tan65°,
解得:x≈3.8cm;
故FG的长度约为3.8cm.
(2)连接OF,
在RT△EFO中,∵EF=20$\sqrt{3}$,EO=20,
∴FO=$\sqrt{E{F}^{2}+E{O}^{2}}$=40,tan∠EOF=$\frac{EF}{EO}$=$\frac{20\sqrt{3}}{20}$=$\sqrt{3}$,
∴∠EOF=60°,
∴∠FOG=∠EOG-∠EOF=5°,
又∵∠GOF′=90°,
∴∠FOF′=85°,
∴点F在旋转过程中所形成的弧的长度为:$\frac{85•π•40}{180}$=$\frac{170π}{9}$cm.
点评 此题主要考查了解直角三角形的应用,充分体现了数学与实际生活的密切联系,解题的关键是表示出线段的长后,理清线段之间的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 110×106 | B. | 11×107 | C. | 1.1×108 | D. | 0.11×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}-2}$ | B. | $\sqrt{-x-2}$ | C. | $\sqrt{x}$ | D. | $\sqrt{{x}^{2}+2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≠1 | B. | x≥-$\frac{1}{2}$且x≠1 | C. | x≥-$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$且x≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7 | B. | 3 | C. | 0 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
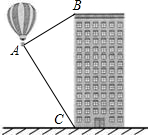 如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )
如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )| A. | 15$\sqrt{3}$ | B. | 30$\sqrt{3}$ | C. | 45$\sqrt{3}$ | D. | 60$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com