
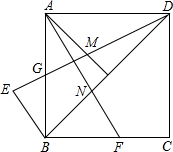
 如图,在正方形ABCD中,G为AB边的中点,∠BAD的平分线交DG于M,过点B作BE⊥BD交DG的延长线于点E,再过点A作AF⊥DG,交BC边于点F,交BD边于点N.
如图,在正方形ABCD中,G为AB边的中点,∠BAD的平分线交DG于M,过点B作BE⊥BD交DG的延长线于点E,再过点A作AF⊥DG,交BC边于点F,交BD边于点N.分析 (1)根据全等三角形的判定和性质得出∠BAG=∠ADM,再证明△ABN与△DAM全等,进而证明即可;
(2)由ASA证明△BEG与△AGM全等,再利用全等三角形的性质得出GM=GE,AM=BE,再证明△AMD与△AEB全等即可;
(3)利用相似三角形的判定和性质进行解答即可.
解答 证明:(1)∵正方形ABCD,
∴AB=AD,∠ABF=∠DAG=90°,
∵AF⊥DG,
∴∠BAF+∠AGD=90°,
∵∠AGD+∠ADG=90°,
∴∠BAF=∠ADG,
在△ADG与△BAF中,
$\left\{\begin{array}{l}{∠BAF=∠ADG}\\{∠DAG=∠ABF=90°}\\{AB=AD}\end{array}\right.$,
∴△ADG≌△BAF(AAS),
∴∠BAG=∠ADM,
∵∠ABN=∠DAM=45°,AB=AD,
在△ABN与△DAM中
$\left\{\begin{array}{l}{AB=AD}\\{∠BAF=∠ADM}\\{∠ABN=∠DAM=45°}\end{array}\right.$,
∴△ABN≌△DAM(AAS),
∴AM=BN,DM=AN;
(2)连接AE,如图: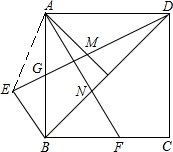
∵∠GAM=∠GBE=45°,∠AGM=∠BGE,AG=BG,
∴△BEG≌△AGM(ASA),
∴GM=GE,AM=BE,
∵∠ABE=∠DAM=45°,BE=AM,AB=AD,
∴△ABE≌△DAM,
∴∠BAE=∠ADM,DM=AE,
∴∠EAM=∠EAB+45°=∠ADM+45°=∠AME,
∴AE=ME,
∴AN=DM=AE=2GM;
(3)连接MN,如图3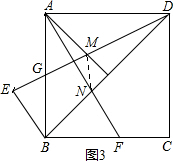
∵∠ADN=∠NBF,∠BNF=∠AND,
∴△ADN~△FBN,
∴$\frac{DN}{BN}=\frac{AD}{BF}=\frac{2}{1}$,
由(2)得:$\frac{DM}{GM}=\frac{2}{1}$,
∴$\frac{DN}{BD}=\frac{DM}{DG}=\frac{2}{3}$,
∵∠MDN=∠GDB,
∴△MDN∽△GDB,
∴$\frac{MN}{BG}=\frac{2}{3}$,
∴$MN=\frac{2}{3}BG=\frac{2}{3}$.
点评 此题考查正方形的性质和全等三角形判定以及性质,关键是根据全等三角形的判定和性质解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有一个二级台阶,每一级的长、宽、高分别为60cm,45cm,27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物,若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?
如图所示,有一个二级台阶,每一级的长、宽、高分别为60cm,45cm,27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物,若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
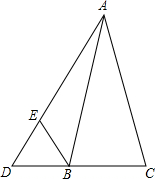 已知,△ABC中,AB=AC,D是CB延长线上的一点,连接AD,∠ADB=60°,在AD上取一点E使AE=CD,求证:△BDE为等边三角形.
已知,△ABC中,AB=AC,D是CB延长线上的一点,连接AD,∠ADB=60°,在AD上取一点E使AE=CD,求证:△BDE为等边三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com