
【题目】在多项式的乘法公式中,完全平方公式![]() 是其中重要的一个.
是其中重要的一个.
(1)请补全完全平方公式的推导过程:
![]() ,
,
![]() ,
,
![]() .
.
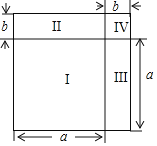
(2)如图,将边长为![]() 的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
(3)用完全平方公式求![]() 的值.
的值.
【答案】(1)ab,ab,2ab;(2)边长为a+b的正方形的面积,等于边长分别为a和b的两个小正方形面积的和,再加上两个长为a,宽为b的长方形的面积,见解析;(3)357604.
【解析】
(1)依据多项式乘多项式法则,即可得到结果;
(2)依据边长为a+b的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,即可得到完全平方公式的几何解释;
(3)利用完全平方公式,即可得到5982的值.
(1)(a+b)2=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
故答案为:ab,ab,2ab;
(2)边长为a+b的正方形的面积,等于边长分别为a和b的两个小正方形面积的和,再加上两个长为a,宽为b的长方形的面积.
(3)5982=[(600+(-2)]2
=6002+2×600×(-2)+(-2)2
=360000-2400+4
=357604.
或5982=(600-2)2
=6002-2×600×2+22
=360000-2400+4
=357604.


科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
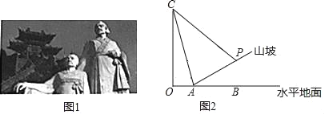
【题目】某游客计划测量这座塑像的高度,(如图1),由于游客无法直接到达塑像底部,因此该游客计划借助坡面高度来测量塑像的高度;如图2,在塑像旁山坡坡脚A处测得塑像头顶C的仰角为75°,当从A处沿坡面行走10米到达P处时,测得塑像头顶C的仰角刚好为45°,已知山坡的坡度i=1:3,且O,A,B在同一直线上,求塑像的高度.(侧倾器高度忽略不计,结果精确到0.1米,参考数据:cos75°≈0.3,tan75°≈3.7,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究,
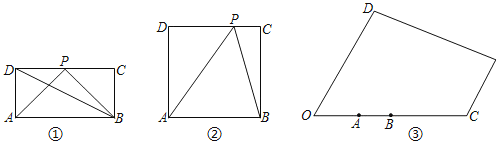
(1)如图①,在矩形ABCD中,AB=2AD,P为CD边上的中点,试比较∠APB和∠ADB的大小关系,并说明理由;
(2)如图②,在正方形ABCD中,P为CD上任意一点,试问当P点位于何处时∠APB最大?并说明理由;
问题解决
(3)某儿童游乐场的平面图如图③所示,场所工作人员想在OD边上点P处安装监控装置,用来监控OC边上的AB段,为了让监控效果最佳,必须要求∠APB最大,已知:∠DOC=60°,OA=400米,AB=200![]() 米,问在OD边上是否存在一点P,使得∠APB最大,若存在,请求出此时OP的长和∠APB的度数;若不存在,请说明理由.
米,问在OD边上是否存在一点P,使得∠APB最大,若存在,请求出此时OP的长和∠APB的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年的春节,对于我们来说,有些不一样,我们不能和小伙伴相约一起玩耍,不能去游乐场放飞自我,也不能和自己的兄弟姐妹一起吃美味的大餐,这么做,是因为我们每一个人都在面临一个眼睛看不到的敌人,它叫病毒,残酷的病毒会让人患上肺炎,人与人的接触会让这种疾病快速地传播开来,严重的还会有生命危险,目前我省已经启动突发公共卫生事件一级应急响应,但我们相信,只要大家一起努力,疫情终有会被战胜的一天.
在这个不能出门的悠长假期里,某小学随机对本校部分学生进行“假期中,我在家可以这么做!A.扎实学习、B.快乐游戏、C.经典阅读、D.分担劳动、E.乐享健康”的网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中的信息,回答下列问题.
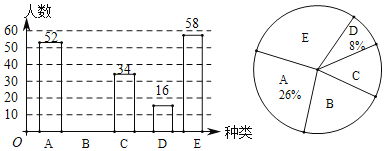
(1)这次调查的总人数是 人;
(2)请补全条形统计图,并说明扇形统计图中E所对应的圆心角是 度;
(3)若学校共有学生的1700人,则选择C有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,点D在BA的延长线上,CD与⊙O交于另一点E,DE=OB=2,∠D=20°,则弧BC的长度为( )
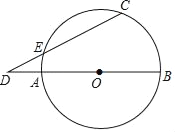
A. ![]() π B.
π B. ![]() π C.
π C. ![]() π D.
π D. ![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,直线L:yax10a与x轴负半轴、y轴正半轴分别交于A、B两点.

(1)当OAOB时,试确定直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AMOQ于M,BNOQ于N,若AM8,BN6,求MN的长.
(3)当a取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角OBF和等腰直角ABE,连接EF交y轴于P点,如图③,问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值,若是,请求出其值,若不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
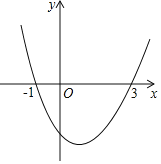
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于(-1,0),(3,0)两点,则下列说法:①abc<0;②a-b+c=0;③2a+b=0;④2a+c>0;⑤若A(x1,y1),B(x2,y2),C(x3,y3)为抛物线上三点,且-1<x1<x2<1,x3>3,则y2<y1<y3,其中正确的结论是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数![]() ,若存在坐标
,若存在坐标![]() 同时满足一次函数
同时满足一次函数![]() 和反比例函数
和反比例函数![]() ,则二次函数
,则二次函数![]() 为一次函数和反比例函数的“共享”函数.
为一次函数和反比例函数的“共享”函数.
(1)试判断(需要写出判断过程):一次函数![]() 和反比例函数
和反比例函数![]() 是否存在“共享”函数?若存在,写出它们的“共享”函数和实数对坐标;
是否存在“共享”函数?若存在,写出它们的“共享”函数和实数对坐标;
(2)已知整数![]() 满足条件:
满足条件:![]() ,并且一次函数
,并且一次函数![]() 与反比例函数
与反比例函数![]() 存在“共享”函数
存在“共享”函数![]() ,求整数
,求整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com