
【题目】如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整.
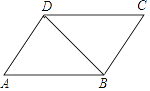
解:∵AD∥CB(已知)
∴∠C+∠ADC=180°(_________________),
又∵∠A=∠C (___________________),
∴∠A+∠ADC=180° (___________________),
∴AB∥CD (___________________________),
∴∠BDC=∠ABD=32° (___________________).
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
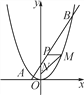
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)已知AE=2,DC=![]() ,求圆弧的半径.
,求圆弧的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
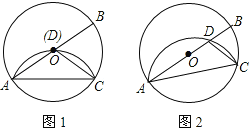
【题目】⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简下列多项式:
(1)![]()
(2)![]()
(3)若![]() ,求
,求![]() 的值.
的值.
(4)先化简,再求值:(2x﹣1)2﹣(3x+1)(3x﹣1)+5x(x﹣1),其中x=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条长为60cm的卷尺铺平后折叠,使得卷尺自身的一部分重合,然后在重合部分(阴影处)沿与卷尺边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度由短到长的比为1:2:3,则折痕对应的刻度的可能性有 ( )
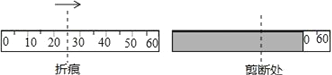
A. 4种 B. 5种 C. 6种 D. 7种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.天气渐热,为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱饮料每降价1元,每天可多售出2箱.针对这种饮料的销售情况,请解答以下问题:
(1)当每箱饮料降价20元时,这种饮料每天销售获利多少元?
(2)在要求每箱饮料获利大于80元的情况下,要使每天销售饮料获利14400元,问每箱应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com