
| A. | 16 | B. | 12 | C. | 12或16 | D. | 无法确定 |
分析 先求出方程x2-7x+12=0的两个根,再根据三角形的三边关系判断出符合题意的菱形的边AB,即可求出菱形的周长,
解答 解:∵x2-7x+12=0,
∴(x-3)(x-4)=0,
∴x1=3,x2=4,
当x1=3时,由菱形的对角线的一条对角线6和菱形的两边3,3不能组成三角形,即不存在菱形,舍去;
当x2=3时,由菱形的对角线的一条对角线6和菱形的两边4,4能组成三角形,即存在菱形,∴菱形的周长为4×4=16.
故选A
点评 此题是菱形的性质题,主要考查了菱形性质,三角形的三边关系,一元二次方程的解法,解本题的关键是确定出菱形的边长,难点是用三角形的三边关系判断符合条件的x的值,也是易错点.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
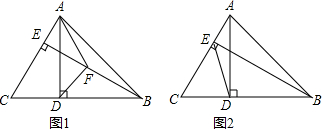
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
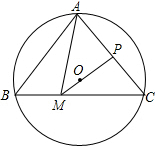 如图,△ABC内接于⊙O,若∠BAC=80°,∠C=50°,取AC中点P,连接PO并延长交BC于点M,连接AM,则∠BAM=( )
如图,△ABC内接于⊙O,若∠BAC=80°,∠C=50°,取AC中点P,连接PO并延长交BC于点M,连接AM,则∠BAM=( )| A. | 45° | B. | 30° | C. | 50° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
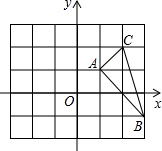 如图,在直角平面坐标系中,△ABC的顶点坐标分别是A(1,1)、B(3,-1)、C(2,2).
如图,在直角平面坐标系中,△ABC的顶点坐标分别是A(1,1)、B(3,-1)、C(2,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
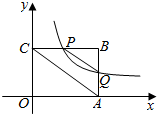 如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线y=$\frac{k}{x}$(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线y=$\frac{k}{x}$(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 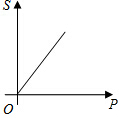 | B. | 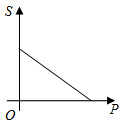 | C. | 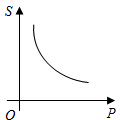 | D. | 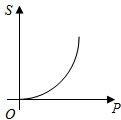 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )| A. | 12 | B. | 24 | C. | 12$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com