
【题目】如图,在矩形ABCD中,过对角线AC的中点O作垂线EF交边BC,AD分别为点E,F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AD=8,AB=4,求CF的长.

【答案】(1)证明见解析;(2)CF=5.
【解析】
(1)根据平行四边形性质推出AD∥BC,根据平行线分线段成比例定理求出OE=OF,推出平行四边形AFCE,根据菱形的判定推出即可;
(2)由矩形的性质得到∠B
为直角,由(1)得AE=CE=CF,设AE=x,则BE=8-x,在直角三角形ABE中,利用勾股定理列出等式,求出x即可.
证明:
∵四边形ABCD是矩形,
∴AD∥BC,∠AFO=∠CEO.
∵点O为AC的中点,
∴AO=OC.
在△AFO和△CEO中,
 ,
,
∴△AFO≌△CEO(AAS),∴OE=OF,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴平行四边形AECF是菱形.
解:
∵四边形ABCD是矩形,
∴∠B=90°.
由(1)知四边形AECF是菱形,
∴设AE=CE=CF=x.则BE=8-x.
在Rt△ABE中,AB2+BE2=AE2,即42+(8-x)2=x2,
解得x=5,
∴CF=5.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
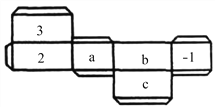
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)+4abc].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为![]() (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为![]() (元),图中折线OAB表示
(元),图中折线OAB表示![]() 与x之间的函数关系.
与x之间的函数关系.
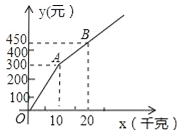
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求![]() 、
、![]() 与x的函数表达式;
与x的函数表达式;
(3)在图中画出![]() 与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D,E,F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )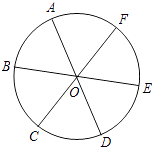
A.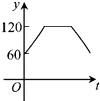
B.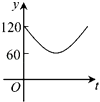
C.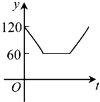
D.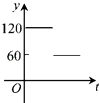
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.

请你结合图中信息,解答下列问题:
(1)本次共调查了 名学生;
(2)被调查的学生中,最喜爱丁类图书的有 人,最喜爱甲类图书的人数占本次被调查人数的 %;
(3)在最喜爱丙类学生的图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
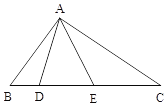
【题目】已知:如图,在△ABC中,点D,E是边BC上的两点,且AB=BE,AC=CD.
(1)若∠BAC =90°,求∠DAE的度数;
(2)若∠BAC=120°,直接写出∠DAE的度数
(3)设∠BAC=α,∠DAE=β,猜想α与β的之间数量关系(不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
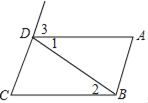
【题目】如图,填空并填写理由:
(1)因为∠1=∠2,所以AD∥BC__________.
(2)因为∠A+∠ABC=180°,所以AD∥BC________.
(3)因为_____∥________,所以∠C+∠ABC=180°(两直线平行,同旁内角互补)
(4)因为______∥______,所以∠3=∠C(两直线平行,同位角相等).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com