
【题目】在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.
(1)如图1,顶点F在边AB上,当CG=OD时,
求m的值;
菱形DEFG是正方形吗?如果是请给予证明.
(2)如图2,连接BF,设CG=a,△FBG的面积为S,求S与a的函数关系式;
(3)如图3,连接GE,当GD平分∠CGE时,请直接写出m的值.

【答案】(1)m=2证明见解析(2)①2;6﹣a(3)m=![]()
【解析】试题分析:(1)将x=0代入y=mx+2得y=2,故此点D的坐标为(0,2),由CG=OD=2可知点G的坐标为(2,6),将点G(2,6)代入y=mx+2可求得m=2;
(2)如图1所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.先证明Rt△GHF≌Rt△EOD,从而得到FH=DO=2,由三角形的面积公式可知:S=6-a.
(3)如图2所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.由菱形的性质可知:DM⊥GM,点M为DF的中点,根据角平分线的性质可知:MD=CD=4,由中点坐标公式可知点M的纵坐标为3,于是得到ND=1,根据勾股定理可求得MN=![]() ,于是得到点M的坐标为(
,于是得到点M的坐标为(![]() ,3)然后利用待定系数法求得DM、GM的解析式,从而可得到点G的坐标,最后将点G的坐标代入y=mx+2可求得m=
,3)然后利用待定系数法求得DM、GM的解析式,从而可得到点G的坐标,最后将点G的坐标代入y=mx+2可求得m=![]() .
.
解:(1)∵将x=0代入y=mx+2得;y=2,∴点D的坐标为(0,2).
∵CG=OD=2,∴点G的坐标为(2,6).
将点G(2,6)代入y=mx+2得:2m+2=6.解得:m=2.
证明△DOE≌△GCD(HL),再证明∠GDE=90°,即可证出菱形GDEF为正方形.
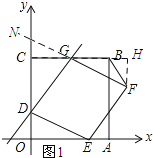
(2)①如图1所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.
∵四边形DEFG为菱形,∴GF=DE,GF∥DE.∴∠GNC=∠EDO.
∴∠NGC=∠DEO.∴∠HGF=∠DEO.
在Rt△GHF和Rt△EOD中,
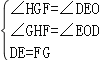 ,
,
∴Rt△GHF≌Rt△EOD.∴FH=DO=2.
∴![]() =
=![]() ×2×(6﹣a)=6﹣a.
×2×(6﹣a)=6﹣a.
(3)如图2所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.
又∵四边形DEFG为菱形,
∴DM⊥GM,点M为DF的中点.
 ∵GD平分∠CGE,DM⊥GM,GC⊥OC,
∵GD平分∠CGE,DM⊥GM,GC⊥OC,
∴MD=CD=4.
∵由(2)可知点F的坐标为4,点D的纵坐标为2,
∴点M的纵坐标为3.
∴ND=1.
在Rt△DNM中,MN=![]() =
=![]() .
.
∴点M的坐标为(![]() ,3).
,3).
设直线DM的解析式为y=kx+2.将(![]() ,3)代入得:
,3)代入得:![]() k+2=3.
k+2=3.
解得:k=![]() .
.
∴设直线MG的解析式为y=![]() x+b.将(
x+b.将(![]() ,3)代入得:﹣15+b=3.
,3)代入得:﹣15+b=3.
解得:b=18.
∴直线MG的解析式为y=﹣![]() x+18.
x+18.
将y=6代入得:![]() .
.
解得:x=![]() .
.
∴点G的坐标为(![]() ,6).
,6).
将(![]() ,6)代入y=mx+2得:
,6)代入y=mx+2得:![]() m+2=6.
m+2=6.
解得:m=![]() .
.


科目:初中数学 来源: 题型:
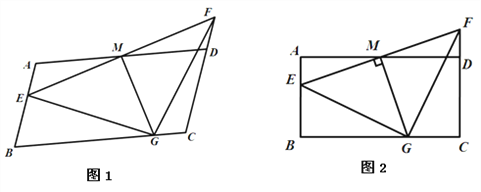
【题目】如图,在平行四边形ABCD中,AB=2,AD=4,M是AD的中点,点E是线段AB上一动点(可以运动到点A和点B),连接EM并延长交线段CD的延长线于点F.
(1) 如图1,①求证:AE=DF; ②若EM=3,∠FEA=45°,过点M作MG⊥EF交线段BC于点G,请直接写出△GEF的的形状,并求出点F到AB边的距离;
(2)改变平行四边形ABCD中∠B的度数,当∠B=90°时,可得到矩形ABCD(如图2),请判断△GEF的形状,并说明理由;
(3)在(2)的条件下,取MG中点P,连接EP,点P随着点E的运动而运动,当点E在线段AB上运动的过程中,请直接写出△EPG的面积S的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)方程(x2)216=0的根为______.
(2)解方程:x24x12=0.
(3)解方程:(3y)2+y2=9.
(4)解方程:2x2+6x-5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
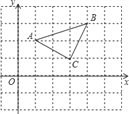
【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图某幢大楼顶部有广告牌CD.张老师目高MA为1.60米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进14米、站在点B处,测得广告牌顶端点C的仰角为45°.(取![]() ,计算结果保留一位小数)
,计算结果保留一位小数)

(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果x2+mx+n=(x+3)(x﹣1),那么m,n的值分别为( )
A. m=2,n=3B. m=2,n=﹣3C. m=﹣2,n=3D. m=﹣2,n=﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com