
【题目】已知,点![]() 为二次函数
为二次函数![]() 图象的顶点,直线
图象的顶点,直线![]() 分别交
分别交![]() 轴正半轴,
轴正半轴,![]() 轴于点
轴于点![]() ,
,![]() .
.
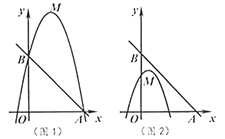
(1)判断顶点![]() 是否在直线
是否在直线![]() 上,并说明理由.
上,并说明理由.
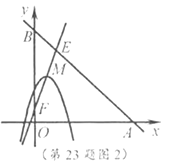
(2)如图1,若二次函数图象也经过点![]() ,
,![]() ,且
,且![]() ,根据图象,写出
,根据图象,写出![]() 的取值范围.
的取值范围.
(3)如图2,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 内,若点
内,若点![]() ,
,![]() 都在二次函数图象上,试比较
都在二次函数图象上,试比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)点![]() 在直线
在直线![]() 上,理由见解析;(2)
上,理由见解析;(2)![]() 的取值范围为
的取值范围为![]() 或
或![]() .(3)①当
.(3)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() .
.
【解析】(1)写出点![]() 的坐标,代入直线
的坐标,代入直线![]() 进行判断即可.
进行判断即可.
(2)直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,求出点
,求出点![]() 坐标,把
坐标,把![]() 在抛物线上,代入求得
在抛物线上,代入求得![]() ,求出二次函数表达式,进而求得点A的坐标,数形结合即可求出
,求出二次函数表达式,进而求得点A的坐标,数形结合即可求出![]() 时,
时,![]() 的取值范围.
的取值范围.
(3)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,而直线
,而直线![]() 表达式为
表达式为![]() ,联立方程组
,联立方程组![]() ,得
,得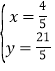 .点
.点![]() ,
,![]() .分三种情况进行讨论.
.分三种情况进行讨论.
【解答】
(1)∵点![]() 坐标是
坐标是![]() ,
,
∴把![]() 代入
代入![]() ,得
,得![]() ,
,
∴点![]() 在直线
在直线![]() 上.
上.
(2)如图1,∵直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,∴点
,∴点![]() 坐标为
坐标为![]() .
.
又∵![]() 在抛物线上,
在抛物线上,
∴![]() ,解得
,解得![]() ,
,
∴二次函数的表达式为![]() ,
,
∴当![]() 时,得
时,得![]() ,
,![]() ,∴
,∴![]() .
.
观察图象可得,当![]() 时,
时,
![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
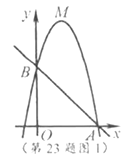
(3)如图2,∵直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
而直线![]() 表达式为
表达式为![]() ,
,
解方程组![]() ,得
,得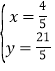 .∴点
.∴点![]() ,
,![]() .
.
∵点![]() 在
在![]() 内,
内,
∴![]() .
.
当点![]() ,
,![]() 关于抛物线对称轴(直线
关于抛物线对称轴(直线![]() )对称时,
)对称时,
![]() ,∴
,∴![]() .
.
且二次函数图象的开口向下,顶点![]() 在直线
在直线![]() 上,
上,
综上:①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】用方程解答下列问题.
(1)一个角的余角比它的补角的![]() 还少15°,求这个角的度数;
还少15°,求这个角的度数;
(2)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问共有多少人?这个物品的价格是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
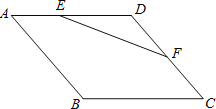
【题目】如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,且AE+CF=4,则△DEF面积的最大值为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
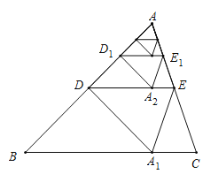
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() ,称为第
,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;还原纸片后,再将
;还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第
处,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;按上述方法不断操作下去…,经过第
;按上述方法不断操作下去…,经过第![]() 次操作后得到的折痕
次操作后得到的折痕![]() ,到
,到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 (单位:克) |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若标准质量为450克,则抽样检测的20袋食品的总质量为多少克?
(3)若该种食品的合格标准为450±5克,求该食品的抽样检测的合格率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,
,![]() 是多项式
是多项式![]() 的一次项系数,
的一次项系数,![]() 是绝对值最小的整数,单项式
是绝对值最小的整数,单项式![]() 的次数为
的次数为![]() .
.
![]()
(1)![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
(2)若将数轴在点![]() 处折叠,则点
处折叠,则点![]() 与点
与点![]() 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向右运动,同时,点
以每秒1个单位长度的速度向右运动,同时,点![]() 和点
和点![]() 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,![]() 秒钟过后,若点
秒钟过后,若点![]() 与点B之间的距离表示为
与点B之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,则
,则![]() = ,
= , ![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(4)请问:AB+BC的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,滑动调节式遮阳伞的立柱![]() 垂直于地面
垂直于地面![]() ,
,![]() 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 位于初始位置
位于初始位置![]() 时,点
时,点![]() 与
与![]() 重合(图2).根据生活经验,当太阳光线与
重合(图2).根据生活经验,当太阳光线与![]() 垂直时,遮阳效果最佳.
垂直时,遮阳效果最佳.
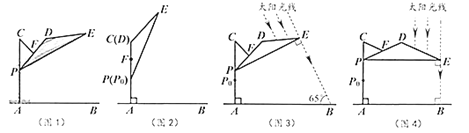
(1)上午10:00时,太阳光线与地面的夹角为![]() (图3),为使遮阳效果最佳,点
(图3),为使遮阳效果最佳,点![]() 需从
需从![]() 上调多少距离?(结果精确到
上调多少距离?(结果精确到![]() )
)
(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点![]() 在(1)的基础上还需上调多少距离?(结果精确到
在(1)的基础上还需上调多少距离?(结果精确到![]() )
)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 、
、![]() ,在平行四边形
,在平行四边形![]() 中,
中,![]() 、
、![]() 的角平分线
的角平分线![]() 、
、![]() 分别与线段
分别与线段![]() 两侧的延长线(或线段
两侧的延长线(或线段![]() )相交与
)相交与![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
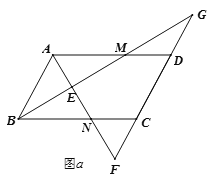
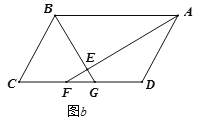
(1)在图![]() 中,求证:
中,求证:![]() ,
,![]() .
.
(2)在图![]() 中,仍有(1)中的
中,仍有(1)中的![]() ,
,![]() 成立,请解答下面问题:
成立,请解答下面问题:
①若![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的长;
的长;
②是否能给平行四边形![]() 的边和角各添加一个条件,使得点
的边和角各添加一个条件,使得点![]() 恰好落在
恰好落在![]() 边上且
边上且![]() 为等腰三角形?若能,请写出所给条件;若不能,请说明理由.
为等腰三角形?若能,请写出所给条件;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com