
 如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B,C,直线BC与坐标轴的交点为D,E.
如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B,C,直线BC与坐标轴的交点为D,E.分析 (1)由条件可先求得A点坐标,从而可求得B点纵坐标,再代入y=$\frac{1}{x}$可求得B点坐标;
(2)可设出A点坐标,从而可表示出C、B的坐标,则可表示出AB和AC的长,可求得△ABC的面积;
(3)可证明△ABC∽△EFC,利用(2)中,AB和AC的长可表示出EF,可得到BG=EF,从而可证明△DBG≌△CFE,可得到DB=CF.
解答 解:
(1)∵点C在y=$\frac{1}{x}$的图象上,且C点横坐标为1,
∴C(1,1),
∵AC∥y轴,AB∥x轴,
∴A点横坐标为1,
∵A点在函数y=$\frac{4}{x}$(x>0)图象上,
∴A(1,4),
∴B点纵坐标为4,
∵点B在y=$\frac{1}{x}$的图象上,
∴B点坐标为($\frac{1}{4}$,4);
(2)设A(a,$\frac{4}{a}$),则C(a,$\frac{1}{a}$),B($\frac{a}{4}$,$\frac{4}{a}$),
∴AB=a-$\frac{a}{4}$=$\frac{3}{4}$a,AC=$\frac{4}{a}$-$\frac{1}{a}$=$\frac{3}{a}$,
∴S△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}$×$\frac{3}{4}$×$\frac{3}{a}$=$\frac{9}{8}$,
即△ABC的面积不发生变化,其面积为$\frac{9}{8}$;
(3)如图,设AB的延长线交y轴于点G,AC的延长线交x轴于点F,
∵AB∥x轴,
∴△ABC∽△EFC,
∴$\frac{AB}{EF}$=$\frac{AC}{FC}$,即$\frac{\frac{3}{4}a}{EF}$=$\frac{\frac{3}{a}}{\frac{1}{a}}$,
∴EF=$\frac{1}{4}$a,
由(2)可知BG=$\frac{1}{4}$a,
∴BG=EF,
∵AE∥y轴,
∴∠BDG=∠FCE,
在△DBG和△CFE中
$\left\{\begin{array}{l}{∠BDG=∠FCE}\\{∠BGD=∠FEC}\\{BG=EF}\end{array}\right.$$\left\{\begin{array}{l}{∠BDG=∠FCE}\\{∠BGD=∠EFC}\\{BG=EF}\end{array}\right.$
∴△DBG≌△CEF(AAS),
∴BD=EF.
点评 本题为反比例函数的综合应用,涉及函数图象的交点、平行线的性质、三角形的面积、相似三角形的判定和性质、全等三角形的判定和性质等知识.要(1)中求得A点坐标是解题的关键,在(2)中用a表示出AB、AC的长是解题的关键,在(3)中证得BG=EF,构造三角形全等是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:选择题
 长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.| A. | 16 | B. | 10 | C. | 18 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
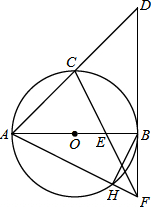 如图,AB是⊙O的直径,C是AD的中点,⊙O的切线BD交AC的延长线于点D,E是OB上一点,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
如图,AB是⊙O的直径,C是AD的中点,⊙O的切线BD交AC的延长线于点D,E是OB上一点,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com