
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,D为AB的中点,E为线段AD上一点,过E点的线段FG交CD的延长线于G点,交AC于F点,且EG=AE.分别延长CE,BG交于点H,若EH平分∠AEG,HD平分∠CHG则下列说法:①∠GDH=45°;②GD=ED;③EF=2DM;④CG=2DE+AE,正确的是( )

A.①②③B.①②④C.②③④D.①②③④
【答案】B
【解析】
首先证明△AEC≌△GEC(SAS),推出CA=CG,∠A=∠CGE=45°,推出DE=DG,故②正确;再证明△EDC≌△GDB,推出∠CED=∠BGD,ED=GD,由三角形外角的性质得出∠HDG=∠HDE,进而得出∠GDH=∠EDH=45°,即可判断①正确;
通过证明△EDC和△EMD是等腰直角三角形,得到ED=![]() MD,再通过证明△EFC≌△EDC,得到EF=ED,从而可判断③错误;由CG=CD+DG,CD=AD,ED=GD,变形即可判断④正确.
MD,再通过证明△EFC≌△EDC,得到EF=ED,从而可判断③错误;由CG=CD+DG,CD=AD,ED=GD,变形即可判断④正确.
∵AC=BC,∠ACB=90°,AD=DB,
∴CD⊥AB,CD=AD=DB,∠A=∠CBD=45°.
∵EH平分∠AEG,
∴∠AEH=∠GEH.
∵∠AEH+∠AEC=180°,∠GEH+∠CEG=180°,
∴∠AEC=∠CEG.
∵AE=GE,EC=EC,
∴△AEC≌△GEC(SAS),
∴CA=CG,∠A=∠CGE=45°.
∵∠EDG=90°,
∴∠DEG=∠DGE=45°,
∴DE=DG,∠AEF=∠DEG=∠A=45°,
故②正确;
∵DE=DG,∠CDE=∠BDG=90°,DC=DB,
∴△EDC≌△GDB(SAS),
∴∠CED=∠BGD,ED=GD.
∵HD平分∠CHG,
∴∠GHD=∠EHD.
∵∠CED=∠EHD+∠HDE,∠BGD=∠GHD+∠HDG,
∴∠HDG=∠HDE.
∵∠EDG=∠ADC=90°,
∴∠GDH=∠EDH=45°,故①正确;
∵∠EDC=90°,ED=GD,
∴△EDC是等腰直角三角形,
∴∠DEG=45°.
∵∠GDH=45°,
∴∠EDH=45°,
∴△EMD是等腰直角三角形,
∴ED=![]() MD.
MD.
∵∠AEF=∠DEG=∠A=45°,
∴∠AFE=∠CFG=90°.
∵∠EDC=90°,
∴∠EFC=∠EDC=90°.
∵EH平分∠AEG,
∴∠AEH=∠GEH.
∵∠FEC=∠GEH,∠DEC=∠AEH,
∴∠FEC=∠DEC.
∵EC=EC,
∴△EFC≌△EDC,
∴EF=ED,
∴EF=![]() MD.
MD.
故③错误;
∵CG=CD+DG=AD+ED=AE+ED+ED,
∴CG=2DE+AE,
故④正确.
故选B.


科目:初中数学 来源: 题型:
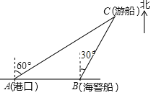
【题目】一艘观光游船从港口![]() 以北偏东
以北偏东![]() 的方向出港观光,航行
的方向出港观光,航行![]() 海里至
海里至![]() 处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东
处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东![]() 方向,马上以
方向,马上以![]() 海里每小时的速度前往救援,海警船到达事故船
海里每小时的速度前往救援,海警船到达事故船![]() 处所需的时间大约为________小时(用根号表示).
处所需的时间大约为________小时(用根号表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC,现有下列结论:①DE=DF; ②DE+DF=AD; ③DM平分∠ADF; ④AB+AC=2AE,其中正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.

(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,点
中,点![]() 是边
是边![]() 上一个动点,过
上一个动点,过![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]()

![]() 的外角平分线于点
的外角平分线于点![]() .
.
![]() 探究:线段
探究:线段![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
![]() 当点
当点![]() 运动到何处,且
运动到何处,且![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?
是正方形?
![]() 当点
当点![]() 在边
在边![]() 上运动时,四边形
上运动时,四边形![]() 会是菱形吗?若是,请证明,若不是,则说明理由.
会是菱形吗?若是,请证明,若不是,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE均为等腰直角三角形,![]() ,B、C、E三点共线,BE平分∠AED,F为CD的中点,AF、AC的延长线分别交DE于H、G点。
,B、C、E三点共线,BE平分∠AED,F为CD的中点,AF、AC的延长线分别交DE于H、G点。
求证:⑴![]() ; ⑵
; ⑵![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求作图:已知A(﹣2,1),B(﹣1,2),C(﹣3,4).

(1)画出与三角形ABC关于y轴对称的三角形A1B1C1;
(2)将三角形A1B1C1先向右平移2个单位,再向下平移1个单位,得到三角形A2B2C2,则三角形A2B2C2顶点坐标分别为:A2 B2 C2 ;
(3)若点P(a,a﹣2)与点Q关于x轴对称,PQ=2,则a的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(-3,-6)的抛物线![]() 经过点(-1,-4),下列结论:①b2>4ac;②ax2+bx+c≥-6;③若点(-2,m),(-5,n)在抛物线上,则m>n;④关于x的一元二次方程
经过点(-1,-4),下列结论:①b2>4ac;②ax2+bx+c≥-6;③若点(-2,m),(-5,n)在抛物线上,则m>n;④关于x的一元二次方程![]() 的两根为﹣5和﹣1,其中正确的有( )
的两根为﹣5和﹣1,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC≌△DEF,并给出证明.
提供的三个条件是:①AB=DE;②AC=DF;③AC∥DF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com