
【题目】若关于x的方程x2﹣mx+n=0没有实数解,则抛物线y=x2﹣mx+n与x轴的交点有( )
A.2个B.1个C.0个D.不能确定
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格如表:
购票人数/人 | 1~50 | 51~100 | 100以上 |
每人门票价/元 | 12 | 10 | 8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题. 我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得 ![]() ,(x、y为正整数)∴
,(x、y为正整数)∴ ![]() 则有0<x<6.又
则有0<x<6.又 ![]() 为正整数,则
为正整数,则 ![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入 ![]() .
.
∴2x+3y=12的正整数解为 ![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:
(2)若 ![]() 为自然数,则满足条件的x值有个;
为自然数,则满足条件的x值有个;
A.2
B.3
C.4
D.5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB经过平移得到线段![]() ,其中点A、B的对应点分别为点
,其中点A、B的对应点分别为点![]() ,
, ![]() ,这四个点都在格点上。若线段AB上有一个点P(a,b),则点P在
,这四个点都在格点上。若线段AB上有一个点P(a,b),则点P在![]() 上的对应点
上的对应点![]() 的坐标为( )
的坐标为( )
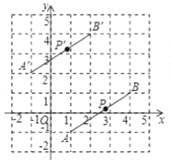
A. (a+2,b﹣3) B. (a+2,b+3) C. (a﹣2,b﹣3) D. (a﹣2,b+3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有13位同学参加学校组织的才艺表演比赛,已知他们所得的分数互不相同,共设7个获奖名额,某同学知道自己的比赛分数后,要判断自己能否获奖,在这13名同学成绩的统计量中只需知道一个量,它是____.(填“众数”“方差”“中位数”或“平均数”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=![]() 的图象交于A(一1,6)、B(a,一2)两点.
的图象交于A(一1,6)、B(a,一2)两点.
(1)求一次函数的解析式;
(2)连接OA、0B,求ΔAOB的面积;
(3)当x满足_______________时, 0<y1≤y2.
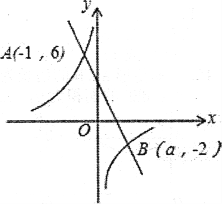
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com