练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．计算：
    （1）a3•（-b3）2+（-2ab2）3；     
    （2）（a-b）10÷（b-a）3÷（b-a）3．

    分析 （1）原式利用积的乘方与幂的乘方法则计算，合并即可得到结果；
    （2）原式变形后，利用同底数幂的除法法则计算即可得到结果．

    解答 解：（1）原式=a3b6-8a3b6=-7a3b6；
    （2）原式=（a-b）10÷（a-b）3÷（a-b）3=（a-b）4．

    点评 此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．计算：
    （1）2-5×0.5-4+3-2×（$\frac{1}{3}$）-3；
    （2）-（$\frac{1}{3}$）2÷（-$\frac{1}{3}$）3×（$\frac{1}{3}$）3÷3-2×（2012）0；
    （3）（-x）3×（x2）5-（-x4）2×（-x）5；
    （4）-5-2-（-5）-1-$\frac{1}{25}$+（-5）-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

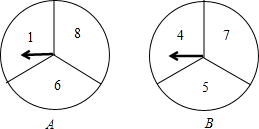    10．如图，设置A、B的转盘分别被分成三个面积相等的扇形，A上的数字分别是1、6、8，B上的数字分别是4、5、7，现两人分别同时转动转盘，当转盘停止转动时，如果我们规定箭头所指较大数字一方获胜，那么你会选择哪个装置．请借助列表法或树状图法说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（-4a3-7a3b2+12a2b）÷（-2a）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算：
    （1）30-2-3+（-3）2-（-$\frac{1}{4}$）-1； 
    （2）（-a2）3-6a2•a4；
    （3）（p-q）4÷（q-p）3•（p-q）2；                 
    （4）（-3ab）（2a2b+ab-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图1，已知直线y=-2x+4与两轴交于A、B两点，抛物线y=x2+bx+c 的顶点M在线段AB上，与y轴交于点C．
    （1）若b=-2，求C点的坐标；
    （2）若△ACM为等腰三角形时，求抛物线的解析式；
    （3）如图2，抛物线的顶点M与B点重合，P为x轴负半轴上一点，过P点作直线l交抛物线于D、E两点，连接BD、BE，试证明：对于x轴负半轴上任意给定的一点P，都存在这样的一条直线l，使得△BPD的面积等于△BDE的面积恒成立．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．关于x的方程2x2+ax+b=0有两个不相等的实数根，且较小的根为2，则下列结论：①ab＜-64；②|a|＜|b|；③抛物线y=2x2+ax+b-1的顶点在第四象限．其中正确的结论是（　　）
    A．①②B．①③C．②③D．①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，在直角坐标系中，已知A（3，0），点B为直线y=$\frac{\sqrt{3}}{3}$x上的一个动点，延长AB至C，使得AB=BC，过点C作CD⊥x轴于点D，交直线OB于点F，过点A作AE∥OB交直线CD于点E．
    （1）若B点的横坐标为6，则DE的长度为2$\sqrt{3}$．
    （2）在点B的运动过程中，线段CF的长度是否发生改变？若不变，请求出线段CF的长度；若改变，请说明理由．
    （3）连接BE，在点B的运动过程中，当△ABE为直角三角形时，求出点E的坐标，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．根据图中提供的信息，求出图中x的值．

    查看答案和解析>>

    同步练习册答案