
【题目】某电子科技公司开发一种新产品,公司对经营的盈亏情况每月最后一天结算1次.在1~12月份中,公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数关系式y=a(x﹣h)2+k,二次函数y=a(x﹣h)2+k的一部分图象如图所示,点A为抛物线的顶点,且点A、B、C的横坐标分别为4、10、12,点A、B的纵坐标分别为﹣16、20.
(1)试确定函数关系式y=a(x﹣h)2+k;
(2)分别求出前9个月公司累计获得的利润以及10月份一个月内所获得的利润;
(3)在前12个月中,哪个月该公司一个月内所获得的利润最多?最多利润是多少万元?
【答案】
(1)解:根据题意可设:y=a(x﹣4)2﹣16,
当x=10时,y=20,
所以a(10﹣4)2﹣16=20,解得a=1,
所求函数关系式为:y=(x﹣4)2﹣16
(2)解:当x=9时,y=(9﹣4)2﹣16=9,所以前9个月公司累计获得的利润为9万元,
又由题意可知,当x=10时,y=20,而20﹣9=11,
所以10月份一个月内所获得的利润11万元
(3)解:设在前12个月中,第n个月该公司一个月内所获得的利润为s(万元)
则有:s=(n﹣4)2﹣16﹣[(n﹣1﹣4)2﹣16]=2n﹣9,
因为s是关于n的一次函数,且2>0,s随着n的增大而增大,
而n的最大值为12,所以当n=12时,s=15,
所以第12月份该公司一个月内所获得的利润最多,最多利润是15万元
【解析】(1)根据题意此抛物线设为y=a(x﹣4)2﹣16,把x=10,y=20,代入即可求得a的值,把a的值代入抛物线的顶点式中即可;(2) 相邻两个月份的总利润的差即为某也利润;(3)根据前x个月所获得的利润减去前x-1个月内所获得的利润,再减去16即可表示出第x个月内所获得的利润,为关于x的一次函数,且为增函数,得到x去最大12时即可求得最多的利润。


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按图中所标注的数据,计算图中实线所围成的面积S是( )

A.50B.62C.65D.68
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的各边分别平行于x轴或y轴,A,B,C,D的坐标分别为(﹣2,1)(2,1)(2,﹣1)(﹣2,﹣1)物体甲和物体乙分别由E(﹣2,0)和F(2,0)同时出发,沿长方形的边按逆时针方向同向行进,甲的速度每秒4个单位长度,乙的速度每秒1个单位长度,则两个物体第2019次相遇地点的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1) 请你判断DA与CE的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )
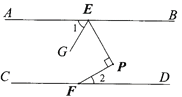
A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)
①画出△ABC关于y轴对称的△A1B1C1 , 并写出点B的对应点B1的坐标;
②画出△ABC向下平移3个单位的△AB2C2 , 并写出点C的对应点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:![]() ;
;
(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com