
 如图,六边形ABCDEF中,AF∥CD,AB∥DE,∠A=140°,∠B=100°,∠E=90°,求:∠C、∠D、∠F的度数.
如图,六边形ABCDEF中,AF∥CD,AB∥DE,∠A=140°,∠B=100°,∠E=90°,求:∠C、∠D、∠F的度数. 分析 连接AD,由AF∥CD得出∠FAD=∠ADC,由AB∥DE得出∠BAD=∠ADE,故可得出∠CDE=∠BAF,∠FAD+∠ADE=∠ADC+∠BAD=$\frac{1}{2}$∠BAF,再由四边形内角和定理即可得出∠F与∠C的度数.
解答 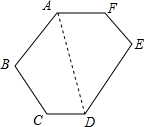 解:连接AD,
解:连接AD,
∵AF∥CD,
∴∠FAD=∠ADC.
∵AB∥DE,
∴∠BAD=∠ADE,
∴∠CDE=∠BAF=140°,
∴∠FAD+∠ADE=∠ADC+∠BAD=∠BAF=140°.
∵∠E=90°,
∴∠F=360°-140°-90°=130°.
∵∠B=100°,
∴∠C=360°-100°-140°=120°.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出内错角是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形OABC和四边形BDEF都是正方形,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点E,若两正方形的面积差为12,则k的值为( )
如图,四边形OABC和四边形BDEF都是正方形,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点E,若两正方形的面积差为12,则k的值为( )| A. | 12 | B. | 6 | C. | -12 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com