
 某中学教学楼的后面靠近一座山坡,坡面下是一块草地,如图所示,BC∥AD,斜坡AB=160米,坡度i=$\sqrt{3}$:1,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造,当坡角不超过45°时可保证山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC进到E处,问BE至少是多少米?(结果保留根号)
某中学教学楼的后面靠近一座山坡,坡面下是一块草地,如图所示,BC∥AD,斜坡AB=160米,坡度i=$\sqrt{3}$:1,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造,当坡角不超过45°时可保证山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC进到E处,问BE至少是多少米?(结果保留根号) 分析 首先过点E作EF⊥AD于F,过点B作BH⊥AD于H,由BC∥AD,可得四边形EFHB是矩形,即可得BE=FH,EF=BH,然后分别在Rt△ABH中与Rt△AEF中,利用三角函数的知识求得AH,AF,EF的长,继而求得答案.
解答 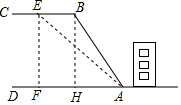 解:过点E作EF⊥AD于F,过点B作BH⊥AD于H,
解:过点E作EF⊥AD于F,过点B作BH⊥AD于H,
∵BC∥AD,
∴四边形EFHB是矩形,
∴EF=BH,BE=FH,
∵斜坡AB=40米,坡度i=$\sqrt{3}$:1,
∴tan∠BAH=$\sqrt{3}$,
∴∠BAH=60°,
在Rt△ABH中,BH=AB•sin∠BAH=40×$\frac{\sqrt{3}}{2}$=20$\sqrt{3}$(米),AH=AB•cos∠BAH=40×$\frac{1}{2}$=20(米),
∴BH=20$\sqrt{3}$米,
∴EF=20$\sqrt{3}$米,
∵∠EAF=45°,
∴在Rt△AEF中,AF=$\frac{EF}{tan∠EAF}$=$\frac{20\sqrt{3}}{1}$=20$\sqrt{3}$(米),
∴BE=FH=AF-AH=20$\sqrt{3}$-20(米).
∴BE至少是(20$\sqrt{3}$-20)米.
点评 此题考查了坡度坡角问题.此题难度适中,注意掌握辅助线的作法,注意能借助于坡度坡角的定义构造直角三角形并解直角三角形是解此题的关键.


科目:初中数学 来源: 题型:选择题
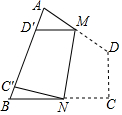 如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
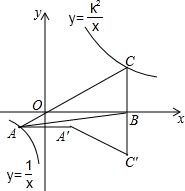 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{k^2}{x}$(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于10.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{k^2}{x}$(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
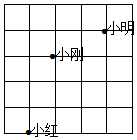 如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )
如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )| A. | (0,0) | B. | (0,1) | C. | (1,0) | D. | (1,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
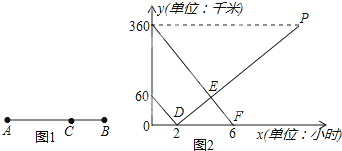
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
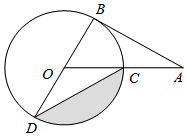 如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )| A. | $\frac{4}{3}π-\sqrt{3}$ | B. | $\frac{4}{3}π-2\sqrt{3}$ | C. | $4π-4\sqrt{3}$ | D. | $\frac{16}{3}π-4\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点O为 Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
如图,点O为 Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com