
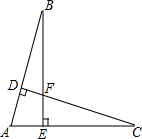
 已知AB=AC,CD⊥AB于点D,BE⊥AC于点E,DC、BE相交于点F.求证:BD=CE.
已知AB=AC,CD⊥AB于点D,BE⊥AC于点E,DC、BE相交于点F.求证:BD=CE.  课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
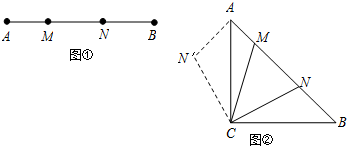
 如图所示,在ABC中,∠C=2∠B,AD是∠CAB的平分线,∠B=∠1,ED=EB,
如图所示,在ABC中,∠C=2∠B,AD是∠CAB的平分线,∠B=∠1,ED=EB,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
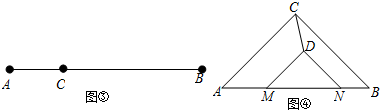
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 靠校园一侧围墙的体育场看台侧面,如图阴影部分所示,看台的三级台阶高度相等,宽度相同,现要用钢管做护栏扶手ACG及三根与水平地面PQ垂直的护栏支架CD、EF和GH(底端D、F、H分别在每级台阶的中点处).已知看台高为1.2米,护栏支架CD=GH=0.8米,∠DCG=66.5°.(参考数据:sin66.5°=0.92,cos66.5°=0.40,tan66.5°=2.30)
靠校园一侧围墙的体育场看台侧面,如图阴影部分所示,看台的三级台阶高度相等,宽度相同,现要用钢管做护栏扶手ACG及三根与水平地面PQ垂直的护栏支架CD、EF和GH(底端D、F、H分别在每级台阶的中点处).已知看台高为1.2米,护栏支架CD=GH=0.8米,∠DCG=66.5°.(参考数据:sin66.5°=0.92,cos66.5°=0.40,tan66.5°=2.30)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
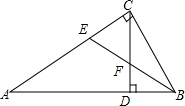 如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )
如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )| A. | ①③④ | B. | ②③④ | C. | ①②④ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com