
����Ŀ����һ�ž���ֽƬ![]() �У�
��![]() ��
��![]() ���ֽ�����ֽƬ������ͼʾ�����۵��������������⣺
���ֽ�����ֽƬ������ͼʾ�����۵��������������⣺
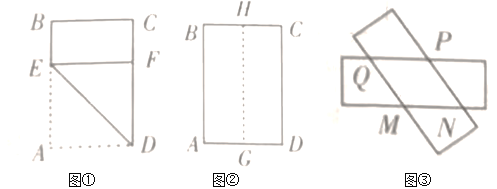
��1����ͼ�٣��ۺ�Ϊ![]() ����
����![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ��
��![]() �ϣ���֤���ı���
�ϣ���֤���ı���![]() �������Σ�
��������
��2����ͼ�ڣ�![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬�Ѿ���ֽƬ
���е㣬�Ѿ���ֽƬ![]() ����
����![]() ������������ž���ֽƬ��������ֽƬ������Ϻ���ͼ�ۣ����ж��ص��ı���
������������ž���ֽƬ��������ֽƬ������Ϻ���ͼ�ۣ����ж��ص��ı���![]() ����״����֤����
����״����֤����
��3���ڣ�2���У��ص��ı���![]() ���ܳ��Ƿ�������ֵ����Сֵ�������ڣ���������ֵ����Сֵ���������ڣ���˵������.
���ܳ��Ƿ�������ֵ����Сֵ�������ڣ���������ֵ����Сֵ���������ڣ���˵������.
���𰸡���1������������2�����Σ�֤������������3����Сֵ12cm�����ֵ20cm.
��������
��1��������һ���ڱ���ȵľ������������ж����ɣ�
��2��������һ���ڱ���ȵ�ƽ���ı����������ж����ɣ�
��3�����ݴ��߶���̺ͽ�������ֵ�Ĺ�ϵ�ж�����.
��:��1�����ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��![]()
���۵������ʿ�֪��![]() ��
��![]() .
.
���ı���![]() �������Σ�
��������
��2���ص��ı���![]() ������
������
֤������ͼ�٣�
����������ֽƬ���Ǿ��Σ����ص��ı��εĶԱ���ƽ�У�
���ı���![]() ��ƽ���ı���.
��ƽ���ı���.

ͼ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
�֡�![]() ��
��![]() .
.
��![]() ��
��
���ı���![]() ������
������
��3�����ݴ��߶���̣��ʵ���������ֽƬ���ഹֱ����ʱ����ͼ�ڣ���������ε��ܳ���СΪ![]() .
.
����![]() ����HNΪ��ֵ������HPNԽС��PN��Խ�ʵ���������ֽƬ����ͼ����ʾ����ʱ���ص����ֵ������ܳ����.
����HNΪ��ֵ������HPNԽС��PN��Խ�ʵ���������ֽƬ����ͼ����ʾ����ʱ���ص����ֵ������ܳ����.


ͼ�� ͼ��
��![]() ����
����![]() .
.
��![]() ��
��![]() ��
��
���![]() .
.
��������ε��ܳ����Ϊ![]() .
.


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д� �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ�����ͼ����x�ύ��A����2��0����B��4��0�����㣬�Һ��������㣨3��10����
��1������κ����Ľ���ʽ��
��2����������κ����Ķ���ΪP������ABP�������
��3����xΪ��ֵʱ��y��0������ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=72�㣬����ABC�Ƶ�B����ʱ�뷽����ת�õ���BDE����D��� A�Ƕ�Ӧ�㣬��E���C�Ƕ�Ӧ�㣩���ұ�DEǡ�þ�����C�����ABD�Ķ���Ϊ

A. 36�� B. 40�� C. 45�� D. 50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��ֱ��MN������A��
��ֱ��MN������A��
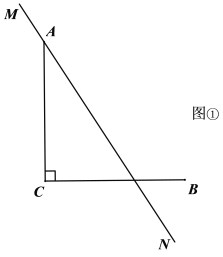
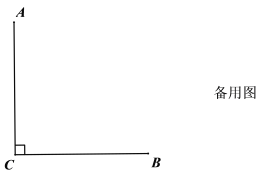
(1)��![]() ������ΪD������CD����ͼ���в�ȫͼ�Σ�����
������ΪD������CD����ͼ���в�ȫͼ�Σ�����![]()
![]() �Ķ�����֤����
�Ķ�����֤����
(2)��ֱ��MN�Ƶ�A��ת�Ĺ����У���![]() ��
�� ![]() ʱ��ֱ��д��DC�ij���
ʱ��ֱ��д��DC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����ı���ABCD��GFED���������Σ���Ȼͼ����AG��CE��AG��CE��
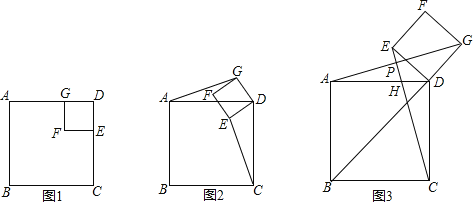
��1����������GFED��D��ת����ͼ2��λ��ʱ��AG��CE�Ƿ�������������������֤����������������˵�����ɣ�
��2����������GFED��D��ת��B��D��G��һ��ֱ�ߣ���ͼ3����ʱ������CE����CE�ֱ�AG��AD��P��H��
����֤��AG��CE��
�������AD��2![]() ��DG��
��DG��![]() ����CE�ij���
����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������е�ÿ��С�����εı߳�����1��ÿ��С�����εĶ�������������ABC����������A��B��C���ڸ����������ABC�Ƶ�A��˳ʱ�뷽����ת90��õ���AB��C����

��1���������������У�������AB��C�䣻
��2�������߶�AB�ڱ任��AB��Ĺ�����ɨ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���BC��Rt��ABC��Rt��DBC�Ĺ���б�ߣ���A��B��C��D����BCΪֱ����Բ�ϣ�����������ĵ㹲Բ������ͼ�ڣ���ABC��������AD��BE��CF�ཻ�ڵ�H����ͼ�������ĵ㹲Բ��������Ϊ��������
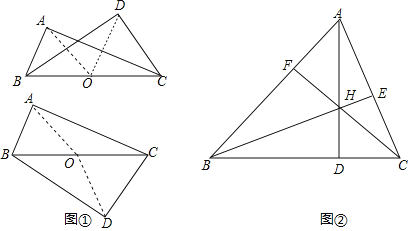
A.2B.3C.4D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C��D���߶�AB�ϣ���PCD�ǵȱ������Σ���CD2��ADBC��
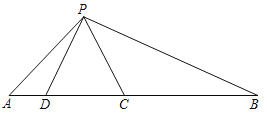
��1����֤����APD�ס�PBC��
��2�����APB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ٵĸ�ĸ�а���һ���ɽ����ֲһ�������������ջ�һ����Ϫ���棬С�ٵĸ�ĸ������mԪ/������ۼ�����5000�����棻ʣ���5000(m��1)�������Ա����ۼ۵�1Ԫ��������������ؿ��̣�Ԥ���ܹ�����55 000Ԫ��ë����

��1����С�ٵĸ�ĸ���깲�ջ��Ϫ������ٽ
��2�������۽�Ϫ����ƽ��ÿ����۳�200�ÿ��ӯ��2Ԫ��Ϊ�˼ӿ����ۺͻ�ýϺõ��ۼۣ���ȡ�˽��۴�ʩ���������۵���ÿ����0.1Ԫ��ƽ��ÿ��ɶ��۳�40�Ӧ���۶���Ԫ��ÿ����������Ϊ600Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com