
����Ŀ��ijУ���꼶ѧ������Ԫ�����������������أ�Ȥζ��ѧ��English World������Ŀ��Ȥζ��ѧ�����ɰ�ƴͼ�����㣬ħ����ԭ���Խת���Լ�����С��Ŀ��ÿλͬѧֻ�ܲμ�һ����Ŀ��С����ͬѧ�Dzμ�Ȥζ��ѧ����Ŀ�����˵���ͳ�ƣ��Ƴ���������ͳ��ͼ�������ݲμӡ�ħ����ԭ����ͬѧ�ijɼ��Ƴ�����������ͳ��ͼ����֪�μ����ɰ�ƴͼ��ͬѧ��24�ˣ��μӡ��Խת�䡱�������Dzμӡ�ħ����ԭ����2���� 
��1���μ�Ȥζ��ѧ��������Ϊ�ˣ�
��2���μӡ�ħ����ԭ��������ռ�μ�Ȥζ��ѧ�������İٷֱ�Ϊ%��
��3����ȫ����ͳ��ͼ��
���𰸡�
��1��120
��2��15
��3���⣺�߲μӡ�ħ����ԭ������18�ˣ�
��μӡ�ħ����ԭ����ͬѧ��ԭħ����ʱ��Ϊ3��4���ӵ��У�18����1+2+3+8��=4���ˣ���
����ͳ��ͼ�������£�

���������⣺��1���߲μ����ɰ�ƴͼ��ͬѧ��24�ˣ�ռ20%��
��μ�Ȥζ��ѧ��������Ϊ24��20%=120���ˣ�����2����μӡ�ħ����ԭ������x�ˣ���μӡ��Խת�䡱����2x�ˣ�
�������x+2x=120����1��25%��20%��10%����
���x=18��
��μӡ�ħ����ԭ��������ռ�μ�Ȥζ��ѧ�������İٷֱ�Ϊ ![]() ��100%=15%��
��100%=15%��
�����㾫�������ڱ��⿼�������ͳ��ͼ������ͳ��ͼ����Ҫ�˽�������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯������ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�����18��35���������ÿ�췢�������ĵ����У���һ���˵ġ��վ�����������Ϊm���涨����m��10ʱΪA������5��m��10ʱΪB������0��m��5ʱΪC�����������ȡ30���������������������˿�չÿ�ˡ��վ������������ĵ��飬���������˵ġ��վ��������������������£�
11 10 6 15 9 16 13 12 0 8
2 8 10 17 6 13 7 5 7 3
12 10 7 11 3 6 8 14 15 12
��1��������������ΪA����Ƶ�ʣ�
��2���Թ���1000��18��35����������С��վ�����������ΪA����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȥ������ȷ���ǣ� ��
A. 3x+(5-2x)=3x+5+2x B. -(x-6)=-x-6
C. 7x-(x+1)=7x-x-1 D. 3(x+8)=3x+8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����λΪ1�ķ���ֽ�ϣ���A1A2A3����A3A4A5����A5A6A7��������б����x���ϡ�б�߳��ֱ�Ϊ2��4��6�����ĵ���ֱ�������Σ�����A1A2A3�Ķ�������ֱ�ΪA1(2��0)��A2(1��-1)��A3(0��0)������ͼ����ʾ���ɣ�A2017�ĺ�����Ϊ�� ��

A. 1010 B. 2 C. 1 D. ��1006
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E�ڶԽ���BD�ϣ��ҡ�BAE=22.5�㣬EF��AB������ΪF����EF�ij�Ϊ��������
A.1
B.![]()
C.4��2![]()
D.3![]() ��4
��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ÿ�����ֱ��ʾ����ľ���ij�����������β���Ӻ��ܰڳ������ε�һ���ǣ� ��
A. 1cm��2cm��3cm B. 2cm��,2cm��4cm
C. 2cm��3cm��4cm D. 1cm��2cm��5cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������һ����ȷ����
A. ͬλ����ȣ���ֱ��ƽ�� B. ���������ε����������
C. ���������εױ��ϵĸ��ߺ�������غ� D. �Զ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD����ABC�Ľ�ƽ���ߣ���ADΪ�ҵġ�O��AB��AC��E��F����֪EF��BC.
��1����֤��BC�ǡ�O�����ߣ�
��2������֪AE=9��CF=4����DE����
��3���ڣ�2���������£�����BAC=60������tan��AFE��ֵ��GD��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧУѧ����ɲ���Уѧ���ᳫ���ġ����С���Ը������г������飬�õ�һ��ѧ�������������ݣ���ͼ�Ǹ����������ݻ��Ƶ�ͳ��ͼ��ͼ�д����Ҹ������θ߶�֮��Ϊ3��4��5��8��2����֪�˴ε����о�15Ԫ��20Ԫ��������39�ˣ�
��1������һ������˶����ˣ�
��2������У����2310��ѧ���������ȫУѧ����������Ԫ��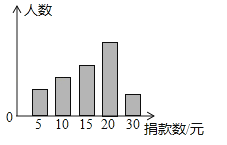
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com