
【题目】已知:如图,点E是正方形ABCD中AD边上的一动点,连结BE,作∠BEG=∠BEA交CD于G,再以B为圆心作![]() ,连结BG.
,连结BG.
(1)求证:EG与![]() 相切.
相切.
(2)求∠EBG的度数.
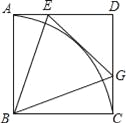
【答案】(1)证明见解析;(2)45°.
【解析】试题分析:(1)过点B作BF⊥EG,垂足为F,先证得△ABE≌△FBE,得出BF=BA,根据切线的判定即可证得结论;
(2)由△ABE≌△FBE得出∠FBE=∠ABE=![]() ∠ABF,然后根据切线长定理得出GF=GC,进而证得∠FBG=∠CBG=
∠ABF,然后根据切线长定理得出GF=GC,进而证得∠FBG=∠CBG=![]() ∠FBC,从而得出∠EBG=
∠FBC,从而得出∠EBG=![]() ∠ABC=45°.
∠ABC=45°.
试题解析:(1)过点B作BF⊥EG,垂足为F,
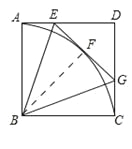
∴∠BFE=90°
∵四边形ABCD是正方形∴∠A=90°,∴∠BFE=∠A,
∵∠BEG=∠BEA,BE=BE, ∴△ABE≌△FBE, ∴BF=BA,
∵BA为![]() 的半径,∴BF为
的半径,∴BF为![]() 的半径,∴EG与
的半径,∴EG与![]() 相切;
相切;
(2)由(1)可得△ABE≌△FBE,∴∠1=∠ABE=![]() ∠ABF,
∠ABF,
∵四边形ABCD是正方形,∴∠C=∠ABC=90°,∴CD是⊙O切线,
由(1)可得EG与![]() 相切,∴GF=GC,
相切,∴GF=GC,
∵BF⊥EG,BC⊥CD,∴∠2=∠CBG=![]() ∠FBC,
∠FBC,
∴∠EBG=∠1+∠2=![]() (∠ABF+∠FBC)=
(∠ABF+∠FBC)= ![]() ∠ABC=45°
∠ABC=45°


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中![]() 为锐角,图2中
为锐角,图2中![]() 为直角,图3中
为直角,图3中![]() 为钝角).
为钝角).

在△ABC的边BC上取![]() ,
, ![]() 两点,使
两点,使![]() ,则
,则![]() ∽
∽![]() ∽
∽![]() ,
, ![]() ,
, ![]() ,进而可得
,进而可得![]()
![]() ;(用
;(用![]() 表示)
表示)
若AB=4,AC=3,BC=6,则![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=![]() ,BE=
,BE=![]() .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-5x+c的图象如图所示.
(1)试求该二次函数的解析式和它的图象的顶点坐标;
(2)观察图象回答,x何值时y的值大于0?
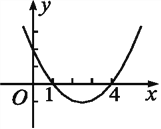
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值及点B的坐标;
(2)求△ABC的面积;
(3)该二次函数图象上有一点D(x,y),使S△ABD=S△ABC,请求出D点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(-1,0),点B在直线![]() 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )
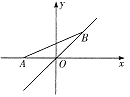
A. (0,0) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com