
 如图,直线AB、CD被直线EF所截,点G,H为它们的交点,∠AGE与它的同位角相等,HP平分∠GHD,∠AGH:∠BGH=3:5,求∠CHG与∠PHD的度数.
如图,直线AB、CD被直线EF所截,点G,H为它们的交点,∠AGE与它的同位角相等,HP平分∠GHD,∠AGH:∠BGH=3:5,求∠CHG与∠PHD的度数. 分析 根据已知条件得到∠AGH=67.5°,由∠AGE与它的同位角相等,得到AB∥CD,根据平行线的性质 得到∠CHG=180°-∠AGH=112.5°,∠GHD=∠AGH=67.5°,然后根据角平分线的性质即可得到结论.
解答 解:∵∠AGH:∠BGH=3:5,∠AGH+∠BGH=180°,
∴∠AGH=67.5°,
∵∠AGE与它的同位角相等,
∴AB∥CD,
∴∠CHG=180°-∠AGH=112.5°,∠GHD=∠AGH=67.5°,
∵HP平分∠GHD,
∴∠PHD=$\frac{1}{2}$∠GHD=33.75°.
点评 本题考查了平行线的性质和判定,熟练掌握平行线的判定和性质是解题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
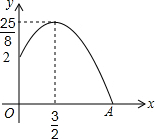 某公园有一喷水池,已知喷水管高2m,喷水最高高度为$\frac{25}{8}$m,此时喷水的水平距离为$\frac{3}{2}$m,求圆形水池的半径.
某公园有一喷水池,已知喷水管高2m,喷水最高高度为$\frac{25}{8}$m,此时喷水的水平距离为$\frac{3}{2}$m,求圆形水池的半径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是由四个长为a、宽为b的长方形围成的空心正方形,其中空心部分也是正方形.
如图,是由四个长为a、宽为b的长方形围成的空心正方形,其中空心部分也是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,∠BAC的平分线AP与BC的垂直平分线PQ相交于点P,过点P分别作PM⊥AC于点M,PN⊥AB交AB延长线于点N,连接PB,PC.求证:BN=CM.
已知:如图,在△ABC中,∠BAC的平分线AP与BC的垂直平分线PQ相交于点P,过点P分别作PM⊥AC于点M,PN⊥AB交AB延长线于点N,连接PB,PC.求证:BN=CM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知正方形DEFG的边DE与等腰直角三角形ABC的斜边AB均在直线l上,点B与点D重合,DE=4,AB=2.若正方形DEFG保持不动,△ABC沿直线l向右以每秒1个单位的速度匀速滑动,试写出从△ABC开始滑动到与正方形DEFG完全脱离开的两图形重叠部分的面积S与滑动时间t的函数表达式.
如图,已知正方形DEFG的边DE与等腰直角三角形ABC的斜边AB均在直线l上,点B与点D重合,DE=4,AB=2.若正方形DEFG保持不动,△ABC沿直线l向右以每秒1个单位的速度匀速滑动,试写出从△ABC开始滑动到与正方形DEFG完全脱离开的两图形重叠部分的面积S与滑动时间t的函数表达式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com