

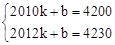 ,解得:
,解得: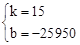 。
。 ,
,

科目:初中数学 来源:不详 题型:解答题
 经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的两根,且
的两根,且 。请解答下列问题:
。请解答下列问题:
 ,求过点P的反比例函数的解析式。
,求过点P的反比例函数的解析式。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 吨,甲、乙两村运往两仓库的荔枝运输费用分别为
吨,甲、乙两村运往两仓库的荔枝运输费用分别为 元和
元和 元.
元. 、
、 与
与 之间的函数关系式;
之间的函数关系式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com