
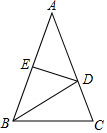
 如图,△ABC中,AB=AC,∠C=2∠A,DE垂直平分AB,交AC于D,交AB于E,求证:AD=BC.
如图,△ABC中,AB=AC,∠C=2∠A,DE垂直平分AB,交AC于D,交AB于E,求证:AD=BC. 分析 先根据△ABC中,AB=AC,∠C=2∠A求出∠A的度数,进而得出∠ABC与∠C的度数,再根据线段垂直平分线的性质得出AD=BD,故可得出∠A=∠ABD,再根据三角形外角的性质即可求出∠CDB的度数,进而得出结论.
解答 解:∵△ABC中,AB=AC,∠C=2∠A,
∴∠ABC=∠C=2∠A,
∴5∠A=180°,解得∠A=36°,
∴∠ABC=∠C=72°,
∵DE是线段AB的垂直平分线,
∴AD=BD,
∴∠A=∠ABD=36°,
∴∠CDB=∠A+∠ABD=72°,
∴∠CDB=∠C,
∴BD=BC,
∴AD=BC.
点评 本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品名 | 黄瓜 | 茄子 |
| 批发价/(元/千克) | 2.4 | 2.2 |
| 零售价/(元/千克) | 3.6 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
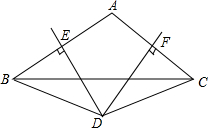 如图,在△ABC中,DE垂直平分AB,DF垂直平分AC.
如图,在△ABC中,DE垂直平分AB,DF垂直平分AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
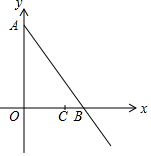 如图:在平面直角坐标系中,点O为坐标原点,△AOB的面积为18$\sqrt{3}$,∠ABO=60°,点C在OB上,OC=4,BC=2,动点P从A点出发沿射线AB以每秒2个单位的速度运动,连接OP.
如图:在平面直角坐标系中,点O为坐标原点,△AOB的面积为18$\sqrt{3}$,∠ABO=60°,点C在OB上,OC=4,BC=2,动点P从A点出发沿射线AB以每秒2个单位的速度运动,连接OP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
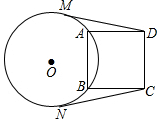 如图,以⊙O的弦AB为边向圆外作正方形ABCD,分别过点D、C作⊙O的切线DM、CN,切点分别为M、N.
如图,以⊙O的弦AB为边向圆外作正方形ABCD,分别过点D、C作⊙O的切线DM、CN,切点分别为M、N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com