
如图,等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为BC边上一点(不与B,C重合),过点P作∠APE=∠B,PE交CD 于E。
(1)求证:△APB∽△PEC;(2)若CE=3,求BP的长。
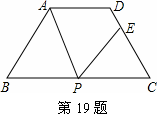
解:(1)证明:梯形ABCD中,∵AD∥BC,AB=DC
∴∠B=∠C=60° ……………1分
∵∠APC=∠B+∠BAP
 即∠APE+∠EPC=∠B+∠BAP
即∠APE+∠EPC=∠B+∠BAP
∵∠APE=∠B
∴∠BAP=∠EPC ……………1分
∴△APB∽△PEC ……………1分
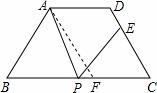
(2)过点A作AF∥CD交BC于F
则四边形ADCF为平行四边形,△ABC为等边三角形 ……………1分
∴CF=AD=3,AB=BF=7-3=4
∵△APB∽△PEC, ……………1分
∴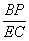 =
=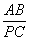
设BP=x,则PC=7-x,又EC=3, AB=4
∴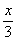 =
=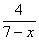 ……………1分
……………1分
整理,得x2-7x+12=0
解得 x1=3, x2=4 ……………1分
经检验, x1=3, x2=4是所列方程的根
∴BP的长为3或4 ……………1分


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
在篮球比赛中,某队员连续10场比赛中每场的得分情况如下表所示:
| 场次(场) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 得分(分) | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 38 |
则这10场比赛中他得分的中位数和众数分别是( )
A.10,4 B.10,7 C.7,13 D.13,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com