练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．已知，如图，AB⊥BD，ED⊥BD，垂足分别为B、D，求证：AC：EC=BC：DC．

    分析 根据AB⊥BD，ED⊥BD，得到AB∥DE，于是得到△ABC∽△EDC，根据相似三角形的性质即可得到结论．

    解答 证明：∵AB⊥BD，ED⊥BD，
    ∴AB∥DE，
    ∴△ABC∽△EDC，
    ∴AC：EC=BC：DC．

    点评 本题考查了相似三角形的判定和性质，平行线的判定，熟练掌握相似三角形的判定和性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．用配方法解下列方程．
    （1）2x2-4x-1=0                          
    （2）ax2+bx+c=0（a≠0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

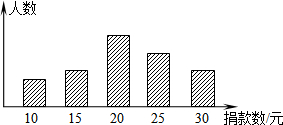    11．振兴中学某班学生对本校学生会倡导的“助学”捐款活动进行抽样调查，得到了一组学生捐款情况的数据．下图是根据这组数据绘制的统计图，图中从左到右各长方形的高度之比为3：4：8：6：4，又知此次调查中捐款20元和25元的学生共28人．
    （1）填空：他们一共调查了50人；第二组（捐款数为15元）的频率为0.16；这组数据的众数是20，中位数是20．
    （2）若该校共有1500名学生，估计全校学生共捐款多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．利用函数图象，求方程$\frac{1}{2}$x2+$\frac{3}{2}$x-2=0的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．已知抛物线y=-2x2-mx+6与x轴两交点间的线段长为4，则m的值是±4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

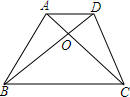    5．如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，且AD：BC=1：2，则下列结论中，错误的是（　　）
    A．S△ABC=S△DBCB．S△AOB=S△CODC．2S△AOD=S△BOCD．2S△AOB=S△BOC

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知函数y=x2+mx+m-2的图象与x轴有两个不同的交点．
    （1）求m的取值范围；
    （2）若抛物线与y轴交于点（0，1），求方程x2+mx+m-2=0的两根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，四边形ABCD是平行四边形，点E为DC延长线上一点，联接AE，交边BC于点F，联接BE．求证：AB•AD=BF•ED．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．在△ABC中，∠A+∠B=150°，∠C=2∠A，则∠A=15°，∠B=135°．

    查看答案和解析>>

    同步练习册答案