
分析 (1)只需将y=-x+3与y=$\frac{2}{x}$组成方程组,并求出该方程组的解即可解决问题;
(2)根据题意得$\left\{\begin{array}{l}{1+n=m+t}\\{2m+2=10m-t}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{n+3}{9}}\\{t=\frac{8n+6}{9}}\end{array}\right.$.然后根据t<n<8m求出n的取值范围,进而求出m的取值范围,就可求出整数m的值;
(3)由a>b>c,a+b+c=0可得a>0,c<0,a>-a-c,-a-c>c,即可得到(2b)2-4ac>0,-2<$\frac{c}{a}$<-$\frac{1}{2}$,由题可得x1+x2=-$\frac{2b}{a}$,x1•x2=$\frac{c}{a}$,从而得到L=$|\begin{array}{l}{{x}_{1}-{x}_{2}}\end{array}|$=$\sqrt{({x}_{1}-{x}_{2})^{2}}$=$\sqrt{({x}_{1+}{x}_{2})^{2}-4{x}_{1}•{x}_{2}}$=2$\sqrt{(\frac{c}{a}+\frac{1}{2})^{2}+\frac{3}{4}}$,利用二次函数的增减性并结合-2<$\frac{c}{a}$<-$\frac{1}{2}$即可得到L的取值范围.
解答 解:(1)联立$\left\{\begin{array}{l}{y=-x+3}\\{y=\frac{2}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
则一次函数y=-x+3和反比例函数y=$\frac{2}{x}$存在“联姻”函数,
它们的“联姻”函数为y=-x2+3x-2,实数对坐标为(1,2),(2,1);
(2)根据题意得:$\left\{\begin{array}{l}{1+n=m+t}\\{2m+2=10m-t}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{n+3}{9}}\\{t=\frac{8n+6}{9}}\end{array}\right.$.
∵t<n<8m,
∴$\left\{\begin{array}{l}{\frac{8n+6}{9}<n}\\{n<\frac{8n+24}{9}}\end{array}\right.$
解得6<n<24,
∴9<n+3<27,
∴1<$\frac{n+3}{9}$<3,
∴1<m<3.
∵m是整数,
∴m=2;
(3)∵a>b>c,a+b+c=0,
∴a>0,c<0,a>-a-c,-a-c>c,
∴(2b)2-4ac>0,-2<$\frac{c}{a}$<-$\frac{1}{2}$,
∴方程ax2+2bx+c=0有两个不相等的实根.
由题可得:x1、x2是方程ax+2b=-$\frac{c}{x}$即ax2+2bx+c=0的两个不等实根.
∴x1+x2=-$\frac{2b}{a}$,x1•x2=$\frac{c}{a}$,
∴L=$|\begin{array}{l}{{x}_{1}-{x}_{2}}\end{array}|$=$\sqrt{({x}_{1}-{x}_{2})^{2}}$=$\sqrt{({x}_{1+}{x}_{2})^{2}-4{x}_{1}•{x}_{2}}$
=$\sqrt{(-\frac{2b}{a})^{2}-4×\frac{c}{a}}$=2$\sqrt{\frac{{b}^{2}-ac}{{a}^{2}}}$
=2$\sqrt{\frac{(-a-c)^{2}-ac}{{a}^{2}}}$=2$\sqrt{\frac{{a}^{2}+ac+{c}^{2}}{{a}^{2}}}$
=2$\sqrt{1+\frac{c}{a}+(\frac{c}{a})^{2}}$
=2$\sqrt{(\frac{c}{a}+\frac{1}{2})^{2}+\frac{3}{4}}$,
∵-2<$\frac{c}{a}$<-$\frac{1}{2}$,
∴$\sqrt{3}$<L<2$\sqrt{3}$.
点评 本题是一道阅读题,主要考查阅读理解能力,在解决问题的过程中用到了解方程组、解不等式组、根与系数的关系、完全平方公式等知识,有一定的难度,运用配方法及二次函数的增减性是解决第(3)小题的关键.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.
在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:
某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
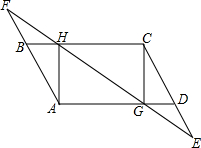 如图,分别延长平行四边形ABCD的边CD、AB到E、F,使DE=BF=$\frac{1}{2}$CD,连接EF,分别交AD,BC于G,H,连接CG,AH
如图,分别延长平行四边形ABCD的边CD、AB到E、F,使DE=BF=$\frac{1}{2}$CD,连接EF,分别交AD,BC于G,H,连接CG,AH查看答案和解析>>
科目:初中数学 来源: 题型:填空题
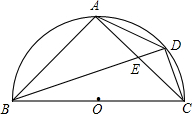 如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.
如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
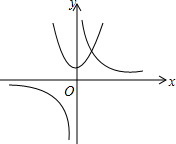 请阅读下列内容:我们在平面直角坐标系中画出抛物线y=x2+1和双曲线y=$\frac{2}{x}$,如图所示,利用两图象的交点个数和位置来确定方程x2+1=$\frac{2}{x}$有一个正实数根,这种方法称为利用的图象判断方程根的情况请用图象法判断方程-(x-3)2+4=$\frac{2}{x}$的根的情况两个正根一个负根(填写根的个数及正负).
请阅读下列内容:我们在平面直角坐标系中画出抛物线y=x2+1和双曲线y=$\frac{2}{x}$,如图所示,利用两图象的交点个数和位置来确定方程x2+1=$\frac{2}{x}$有一个正实数根,这种方法称为利用的图象判断方程根的情况请用图象法判断方程-(x-3)2+4=$\frac{2}{x}$的根的情况两个正根一个负根(填写根的个数及正负).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com