
【题目】如图,抛物线 ![]() 与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.
与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.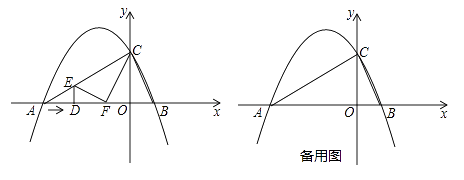
(1)求抛物线的解析式和对称轴;
(2)是否存在某一时刻t,使得△EFC为直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)设四边形DECO的面积为s,求s关于t的函数表达式.
【答案】
(1)解:把A(﹣4,0),B(1,0),点C(0,2)代入 ![]() 得:
得:  ,解得:
,解得:  ,
,
∴抛物线的解析式为: ![]() ,
,
对称轴为:直线x=﹣ ![]() ;
;
(2)解:存在,∵AD=2t,
∴DF=AD=2t,
∴OF=4﹣4t,
∴D(2t﹣4,0),
∵直线AC的解析式为: ![]() ,∴E(2t﹣4,t),
,∴E(2t﹣4,t),
∵△EFC为直角三角形,分三种情况讨论:
① 当∠EFC=90°,则△DEF∽△OFC,
∴ ![]() ,即
,即 ![]() ,解得:t=
,解得:t= ![]() ;
;
②当∠FEC=90°,
∴∠AEF=90°,
∴△AEF是等腰直角三角形,
∴DE= ![]() AF,即t=2t,
AF,即t=2t,
∴t=0,(舍去),
③当∠ACF=90°,则AC2+CF2=AF2 , 即(42+22)+[22+(4t﹣4)2]=(4t)2 , 解得:t= ![]() ,
,
∴存在某一时刻t,使得△EFC为直角三角形,此时,t= ![]() 或
或 ![]() ;
;
(3)解:∵B(1,0),C(0,2),
∴直线BC的解析式为:y=﹣2x+2,
当D在y轴的左侧时,S= ![]() (DE+OC)OD=
(DE+OC)OD= ![]() (t+2)(4﹣2t)=﹣t2+4 (0<t<2);
(t+2)(4﹣2t)=﹣t2+4 (0<t<2);
当D在y轴的右侧时,如图2,
∵OD=4t﹣4,DE=﹣8t+10,S= ![]() (DE+OC)OD=
(DE+OC)OD= ![]() (﹣8t+10+2)(4t﹣4),即
(﹣8t+10+2)(4t﹣4),即 ![]() (2<t<
(2<t< ![]() ).
).
综上所述: 
【解析】(1)(1)利用待定系数法,将点A、B、C的坐标代入函数解析式,建立方程组求解即可。
(2)根据题意分别求出AD、DF、OF的长,表示出点D的坐标,利用待定系数法求出直线BC的函数解析式,表示出点E的坐标,再分三种情况讨论△EFC为直角三角形:① 当∠EFC=90°,则△DEF∽△OFC,根据相似三角形的性质,列出关于t的方程求解即可;②∠FEC=90°,∠AEF=90°,△AEF是等腰直角三角形求出t的值即可;③当∠ACF=90°,则AC2+CF2=AF2 , 建立关于t的方程求解即可,从而可得出答案。
(3)求得直线BC的解析式为:y=-2x+2,当D在y轴的左侧时,当D在y轴的右侧时,如图2,根据梯形的面积公式即可得到结论。


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE. 
(1)求证:AE=BD;
(2)求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”.
例如:2635,x=2+6,y=3+5,因为x=y,所以2635是“和平数”.
(1)请判断:3562 (填“是”或“不是”)“和平数”.
(2)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(3)如果一个“和平数”的个位上的数字是千位上的数字的两倍,且百位上的数字与十位上的数字之和是14,求满足条件的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
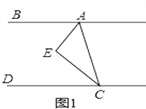
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )

①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题,原命题和它的逆命题都是真命题的是( )
A.若![]() ,则
,则![]()
B.若三角形的三条边分别为![]() ,则这个三角形是直角三角形
,则这个三角形是直角三角形
C.正方形的四条边都相等
D.对角线互相垂直平分的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角△ABC中,AB=AC,∠BAC=90°,过点B,点C分别作经过点A的直线l的垂线,垂足分别为M、N.
(1)请找到一对全等三角形,并说明理由;
(2)BM,CN,MN之间有何数量关系?并说明理由;
(3)若BM=3,CN=5,求四边形MNCB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )

A. 4m厘米 B. 4n厘米 C. 2(m+n)厘米 D. 4(m-n)厘米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com