
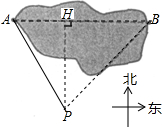
 在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.)
在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.) 分析 作PH⊥AB于点H,在直角△APH中求得HP和AH的长,然后在直角△BPH中利用三角函数求得BH的长,根据AB=AH+BH即可求解.
解答 解:作PH⊥AB于点H.
∵在直角△APH中,∠APH=30°,
∴AH=$\frac{1}{2}$AP=$\frac{1}{2}$×400=200(米),PH=AP•cos∠APH=400×$\frac{\sqrt{3}}{2}$=200$\sqrt{3}$(米),
又∵直角△PBH中,∠BPH=43°,
∴BH=PH•tan∠BPH=200$\sqrt{3}$×tan43°≈200$\sqrt{3}$×0.93=186$\sqrt{3}$(米),
则AB=AH+BH=200+186$\sqrt{3}$≈200+186×1.7=516.2≈516(米).
答:码头A与亭子B之间的距离是516米.
点评 本题考查了解直角三角形,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:填空题
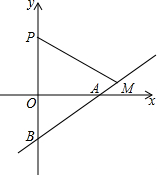 如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
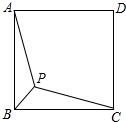 如图,点P是正方形ABCD内一点,连接AP、BP、CP,若BP=$\sqrt{3}$,CP=$\sqrt{30}$,∠BPA=135°,则正方形ABCD的边长为$\sqrt{39}$.
如图,点P是正方形ABCD内一点,连接AP、BP、CP,若BP=$\sqrt{3}$,CP=$\sqrt{30}$,∠BPA=135°,则正方形ABCD的边长为$\sqrt{39}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
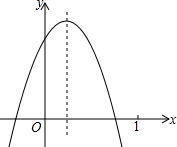 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①方程ax2+bx+c=0的两根之和大于0; ②a+b<0;③y随x的增大而增大;④a-b+c<0,⑤2a-b>0. 其中正确的个数( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①方程ax2+bx+c=0的两根之和大于0; ②a+b<0;③y随x的增大而增大;④a-b+c<0,⑤2a-b>0. 其中正确的个数( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
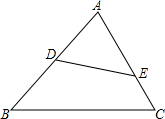 如图,已知D、E分别在△ABC的边AB、AC上,D为AB的中点,AE:EC=2:1,△ADE∽△ACB,且∠ADE=∠C,求$\frac{DE}{BC}$的值.
如图,已知D、E分别在△ABC的边AB、AC上,D为AB的中点,AE:EC=2:1,△ADE∽△ACB,且∠ADE=∠C,求$\frac{DE}{BC}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
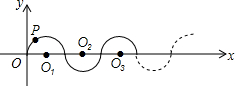 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是( )
如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是( )| A. | (2014,0) | B. | (2015,-1) | C. | (2015,1) | D. | (2016,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com