
【题目】完成下面的推理.
已知:如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.
试说明:∠EGF=90°.
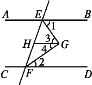
解:因为HG∥AB(已知),
所以∠1=∠3( ).
又因为HG∥CD(已知),
所以∠2=∠4( ).
因为AB∥CD(已知),
所以∠BEF+ =180°( ).
又因为EG平分∠BEF(已知),
所以∠1=![]() ∠ ( ).
∠ ( ).
又因为FG平分∠EFD(已知),
所以∠2=![]() ∠ ( ),
∠ ( ),
所以∠1+∠2=![]() ( + ).
( + ).
所以∠1+∠2=90°.
所以∠3+∠4=90°( ),即∠EGF=90°.
【答案】两直线平行,内错角相等;两直线平行,内错角相等;∠EFD;两直线平行,同旁内角互补;∠BEF;角平分线定义;∠EFD;角平分线定义;∠BEF;∠EFD;等量代换.
【解析】
依据平行线的性质和判定定理以及角平分线的定义,结合解答过程进行填空即可.
∵AB∥GH(已知),
∴∠1=∠3(两直线平行,内错角相等),
又∵CD∥GH(已知),
∴∠2=∠4(两直线平行,内错角相等).
∵AB∥CD(已知),
∴∠BEF+∠EFD=180°(两直线平行,同旁内角互补).
∵EG平分∠BEF(已知),
∴∠1=![]() ∠BEF(角平分线定义),
∠BEF(角平分线定义),
又∵FG平分∠EFD(已知),
∴∠2=![]() ∠EFD(角平分线定义),
∠EFD(角平分线定义),
∴∠1+∠2=![]() (∠BEF+∠EFD),
(∠BEF+∠EFD),
∴∠l+∠2=90°,
∴∠3+∠4=90°(等量代换),
即∠EGF=90°.
故答案为:两直线平行,内错角相等;两直线平行,内错角相等;∠EFD;两直线平行,同旁内角互补;∠BEF;角平分线定义;∠EFD;角平分线定义;∠BEF;∠EFD;等量代换.


科目:初中数学 来源: 题型:
【题目】设双曲线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在第三象限),将双曲线在第一象限的一支沿射线
在第三象限),将双曲线在第一象限的一支沿射线![]() 的方向平移,使其经过点
的方向平移,使其经过点![]() ,将双曲线在第三象限的一支沿射线
,将双曲线在第三象限的一支沿射线![]() 的方向平移,使其经过点
的方向平移,使其经过点![]() ,平移后的两条曲线相交于点
,平移后的两条曲线相交于点![]() ,
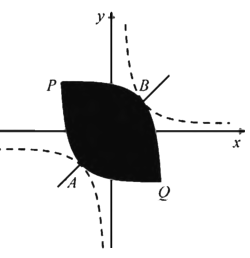
,![]() 两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,
两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,![]() 为双曲线的“眸径”.当双曲线
为双曲线的“眸径”.当双曲线![]() 的眸径为6时,
的眸径为6时,![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.

(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若tan∠P=![]() ,AD=6,求线段AE的长.
,AD=6,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
如图,根据给出的数轴,解答下面的问题:
![]()
(1)已知点![]() 表示的数分别为6,-4,观察数轴,与点
表示的数分别为6,-4,观察数轴,与点![]() 距离为5的点所表示的数是 ,
距离为5的点所表示的数是 ,![]() 两点之间的距离为 ;
两点之间的距离为 ;
(2)若点![]() 到点
到点![]() ,点
,点![]() 的距离相等,观察数轴并结合所学知识求点
的距离相等,观察数轴并结合所学知识求点![]() 表示的数;
表示的数;
(3)在(2)的条件下,若动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() 秒.则点
秒.则点![]() 表示的数是多少(用含字母
表示的数是多少(用含字母![]() 的式子表示);当
的式子表示);当![]() 等于多少秒时,
等于多少秒时,![]() 之间的距离为3个单位长度.
之间的距离为3个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有![]() 、
、![]() 、
、![]() 三个点,它们表示的数分别是
三个点,它们表示的数分别是![]() ,
,![]() ,10,我们约定点
,10,我们约定点![]() 与点
与点![]() 之间的距离记为
之间的距离记为![]() ,点
,点![]() 与点
与点![]() 之间的距离记为
之间的距离记为![]() .
.
(1)线段![]() 的长度为 ,线段
的长度为 ,线段![]() 的长度为 ;
的长度为 ;
(2)若点![]() 向左运动6个单位长度,则运动后的点表示的数为 ;若点
向左运动6个单位长度,则运动后的点表示的数为 ;若点![]() 向右运动6个单位长度,则运动后的点表示的数为 ;
向右运动6个单位长度,则运动后的点表示的数为 ;
(3)若点![]() 以每秒1个单位长度的速度向左运动,同时点
以每秒1个单位长度的速度向左运动,同时点![]() 和点
和点![]() 分别以每秒3个单位长度和7个单位长度的速度向右运动,设运动时间为
分别以每秒3个单位长度和7个单位长度的速度向右运动,设运动时间为![]() 秒.
秒.
①试用含![]() 的式子分别表示点
的式子分别表示点![]() 、
、![]() 、
、![]() 运动
运动![]() 秒后的位置所对应的数;
秒后的位置所对应的数;
![]()
![]()
![]()
②试探索:![]() 的值是否为定值?若是,请求出其定值;若不是,请说明理由.
的值是否为定值?若是,请求出其定值;若不是,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列所给条件中,不能判断两个直角三角形全等的是( )
A. 一个锐角和这个锐角的对边对应相等B. 一个锐角与斜边对应相等
C. 两锐角对应相等D. 一锐角和一边对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、以两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.
(1)用画树状图或列表的方法列出所有可能的结果;
(2)这样的游戏规则是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
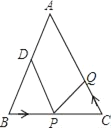
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com