
分析 (1)利用平方差公式计算;
(2)先化简合并,再算除法;
(3)先算负指数幂,利用平方差公式计算,再进一步合并即可;
(4)先算乘方、负指数幂、0指数幂,以及利用根式的化简,再进一步合并即可;
(5)(6)利用二次根式的运算方法计算化简,再进一步合并即可.
解答 解:(1)原式=12-6
=6;
(2)原式=(8$\sqrt{3}$-9$\sqrt{3}$)÷$\sqrt{6}$
=-$\sqrt{3}$÷$\sqrt{6}$
=-$\frac{\sqrt{2}}{2}$;
(3)原式=5+1-3-2$\sqrt{3}$
=3-2$\sqrt{3}$;
(4)原式=-1+1+2-($\sqrt{2}$-1)
=3-$\sqrt{2}$;
(5)原式=$\sqrt{6}$-3-2$\sqrt{6}$-3+$\sqrt{6}$
=-6;
(6)原式=-8$\sqrt{2}$+9$\sqrt{2}$-12-1+3$\sqrt{2}$
=4$\sqrt{2}$-13.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
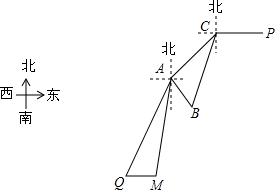 南沙群岛自古以来都是中国领土,如图,点A、B、C分别表示南沙群岛的三个小岛,岛C在岛A的北偏东45°方向,岛B在岛C的南偏西15°方向上,岛B在岛A的南偏东30°方向,且岛A、岛B两岛的距离为3海里.
南沙群岛自古以来都是中国领土,如图,点A、B、C分别表示南沙群岛的三个小岛,岛C在岛A的北偏东45°方向,岛B在岛C的南偏西15°方向上,岛B在岛A的南偏东30°方向,且岛A、岛B两岛的距离为3海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
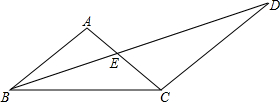 如图,△ABC中AB=AC=10,BC=16.
如图,△ABC中AB=AC=10,BC=16.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com