
分析 先根据分式的乘法法则把原式进行化简,再求出x、y的值代入进行计算即可.
解答 解:原式=$\frac{x(x+y)}{(x-y)^{2}}$•$\frac{(x+y)(x-y)}{(x+y)^{2}}$
=$\frac{x(x+y)}{(x-y)^{2}}$•$\frac{x-y}{x+y}$
=$\frac{x}{x-y}$.
∵解方程组$\left\{\begin{array}{l}{x+2y=1}\\{x-y=4}\end{array}\right.$得,$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$,
∴原式=$\frac{3}{3+1}$=$\frac{3}{4}$.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.


科目:初中数学 来源: 题型:解答题
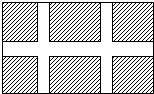 如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
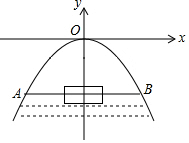 如图,一抛物线拱桥,拱顶O离水面高4米,水面宽度AB=10米,现有一竹排运送一只货箱欲从桥下通过,已知货箱长10米,宽6米,高2.5米(竹排与水面持平),问货箱能否顺利通过该桥?
如图,一抛物线拱桥,拱顶O离水面高4米,水面宽度AB=10米,现有一竹排运送一只货箱欲从桥下通过,已知货箱长10米,宽6米,高2.5米(竹排与水面持平),问货箱能否顺利通过该桥?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com